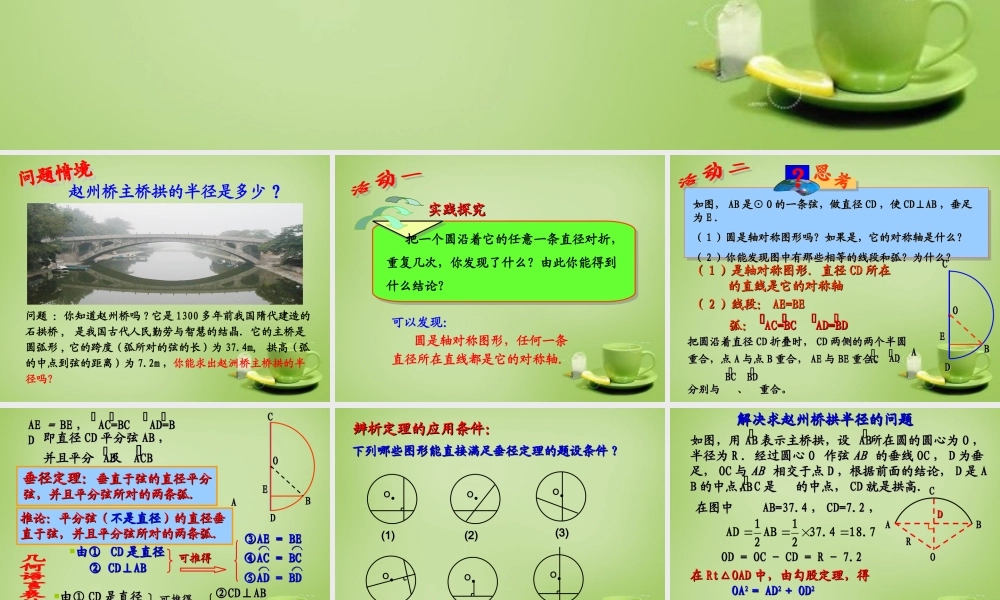
问题 :你知道赵州桥吗 ? 它是 1300 多年前我国隋代建造的石拱桥 , 是我国古代人民勤劳与智慧的结晶.它的主桥是圆弧形 , 它的跨度 ( 弧所对的弦的长 ) 为 37.4m, 拱高 ( 弧的中点到弦的距离 ) 为 7.2m ,你能求出赵洲桥主桥拱的半径吗? 赵州桥主桥拱的半径是多少? 实践探究实践探究 把一个圆沿着它的任意一条直径对折,重复几次,你发现了什么?由此你能得到什么结论?可以发现: 圆是轴对称图形,任何一条直径所在直线都是它的对称轴. 如图,如图, ABAB 是⊙是⊙ OO 的一条弦,做直径的一条弦,做直径 CDCD ,使,使 CD⊥ABCD⊥AB ,垂足,垂足为为 EE ..(( 11 )圆是轴对称图形吗?如果是,它的对称轴是什么?)圆是轴对称图形吗?如果是,它的对称轴是什么?(( 22 )你能发现图中有那些相等的线段和弧?为什么?)你能发现图中有那些相等的线段和弧?为什么?·OOAABBCCDDEE(( 11 )是轴对称图形.直径)是轴对称图形.直径 CDCD 所在所在 的直线是它的对称轴的直线是它的对称轴(( 22 )线段:)线段: AE=BEAE=BE弧: 弧: AC=BC AD=BDAC=BC AD=BD⌒⌒⌒⌒⌒⌒⌒⌒把圆沿着直径把圆沿着直径 CDCD 折叠时,折叠时, CDCD 两侧的两个半圆两侧的两个半圆重合,点重合,点 AA 与点与点 BB 重合,重合, AEAE 与与 BEBE 重合, 、 重合, 、 分别与 、 重合分别与 、 重合。⌒⌒ACAC⌒⌒ADAD⌒⌒BCBC⌒⌒BDBD·OOAABBCCDDEE垂径定理:垂径定理:垂直于弦的直径平分垂直于弦的直径平分弦,并且平分弦所对的两条弧.弦,并且平分弦所对的两条弧.推论:平分弦(推论:平分弦(不是直径不是直径)的直径垂)的直径垂直于弦,并且平分弦所对的两条弧.直于弦,并且平分弦所对的两条弧.AEAE == BEBE , , AC=BC AD=BAC=BC AD=BDD ⌒⌒⌒⌒⌒⌒⌒⌒即直径即直径 CDCD 平分弦平分弦 ABAB ,,并且平分并且平分及及⌒⌒ACBACB⌒⌒ABAB由① 由① CDCD 是直径是直径② ② CD⊥ABCD⊥AB可推得可推得③③AE = BE AE = BE ⌒⌒⌒⌒④④AC = BCAC = BC⌒⌒⌒⌒⑤⑤AD = BDAD = BD③③AE = BE AE = BE 由①由① CDCD 是直径是直径可推得可推得②②CD⊥ABCD⊥AB⌒⌒⌒⌒⑤⑤AD = BDAD = BD⌒⌒⌒⌒④④AC = BCAC = BC辨析定理的应用条件:辨析定理的应用条件:下列哪些图形能直接满足垂径定理的题设条件下列哪些图...