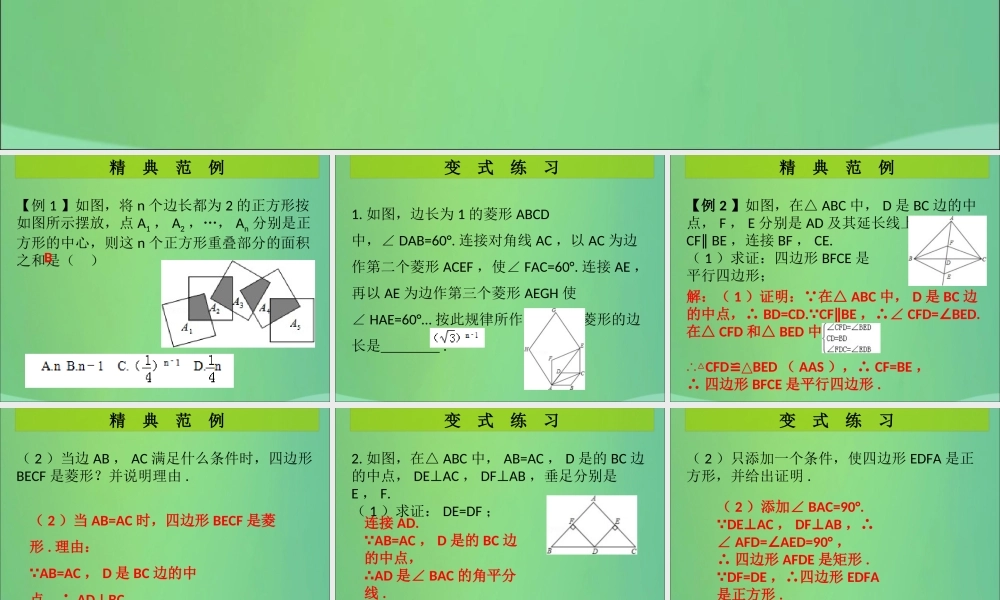
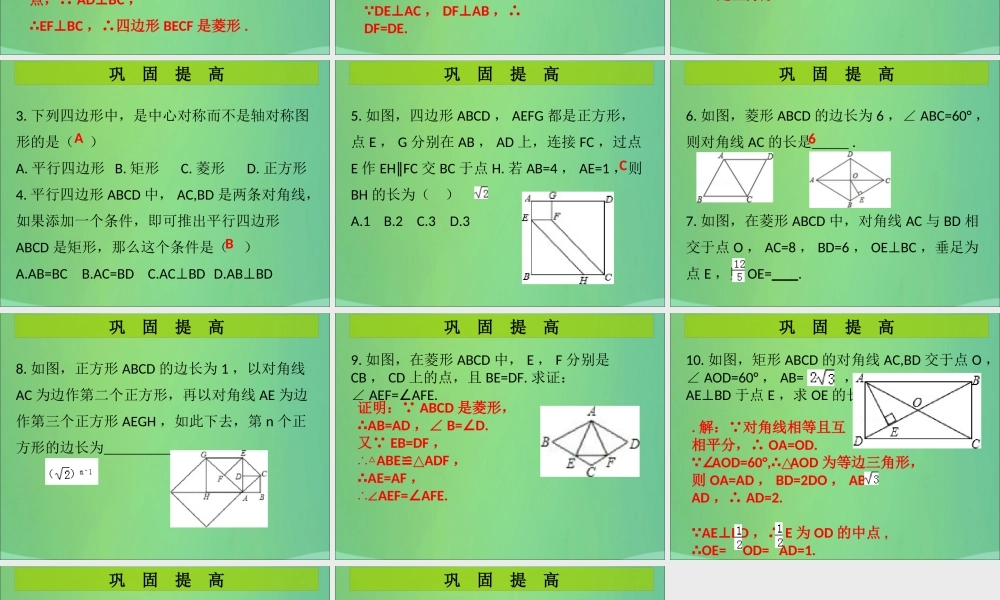
巩固提高精典范例(变式练习)第 9 课时 《特殊平行四边形》单元复习第一章 特殊的平行四边形【例 1 】如图,将 n 个边长都为 2 的正方形按如图所示摆放,点 A1 , A2 ,…, An 分别是正方形的中心,则这 n 个正方形重叠部分的面积之和是( )精 典 范 例B1. 如图,边长为 1 的菱形 ABCD中,∠ DAB=60°. 连接对角线 AC ,以 AC 为边作第二个菱形 ACEF ,使∠ FAC=60°. 连接 AE ,再以 AE 为边作第三个菱形 AEGH 使∠ HAE=60°… 按此规律所作的第 n 个菱形的边长是 .变 式 练 习【例 2 】如图,在△ ABC 中, D 是 BC 边的中点, F , E 分别是 AD 及其延长线上的点,CF∥ BE ,连接 BF , CE.( 1 )求证:四边形 BFCE 是平行四边形;精 典 范 例解:( 1 )证明: 在△ ABC 中, D 是 BC 边的中点,∴ BD=CD. CF BE∥,∴∠ CFD=BED.∠在△ CFD 和△ BED 中,,∴△CFDBED≌△( AAS ),∴ CF=BE ,∴ 四边形 BFCE 是平行四边形 .( 2 )当边 AB , AC 满足什么条件时,四边形BECF 是菱形?并说明理由 .精 典 范 例( 2 )当 AB=AC 时,四边形 BECF 是菱形 . 理由: AB=AC , D 是 BC 边的中点,∴ ADBC⊥,∴EFBC⊥,∴四边形 BECF 是菱形 .2. 如图,在△ ABC 中, AB=AC , D 是的 BC 边的中点, DEAC⊥, DFAB⊥,垂足分别是E , F.( 1 )求证: DE=DF ;变 式 练 习连接 AD. AB=AC , D 是的 BC 边的中点,∴AD 是∠ BAC 的角平分线 . DEAC⊥, DFAB⊥,∴DF=DE.( 2 )只添加一个条件,使四边形 EDFA 是正方形,并给出证明 .变 式 练 习( 2 )添加∠ BAC=90°. DEAC⊥, DFAB⊥,∴∠ AFD=AED=90°∠,∴ 四边形 AFDE 是矩形 . DF=DE ,∴四边形 EDFA是正方形 .巩 固 提 高3. 下列四边形中,是中心对称而不是轴对称图形的是( )A. 平行四边形 B. 矩形C. 菱形D. 正方形4. 平行四边形 ABCD 中, AC,BD 是两条对角线,如果添加一个条件,即可推出平行四边形ABCD 是矩形,那么这个条件是( )A.AB=BCB.AC=BDC.ACBD⊥D.ABBD⊥AB巩 固 提 高5. 如图,四边形 ABCD , AEFG 都是正方形,点 E , G 分别在 AB , AD 上,连接 FC ,过点E 作 EH FC∥交 BC 于点 H. 若 AB=4 , AE=1 ,则BH 的长...