人教版高一数学三角函数的定义 课件VIP免费

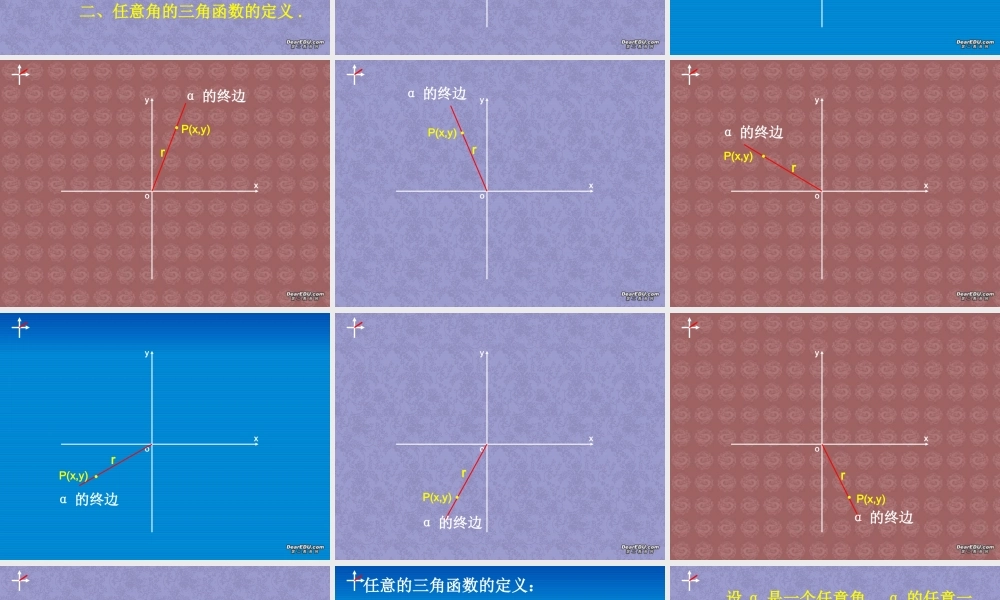
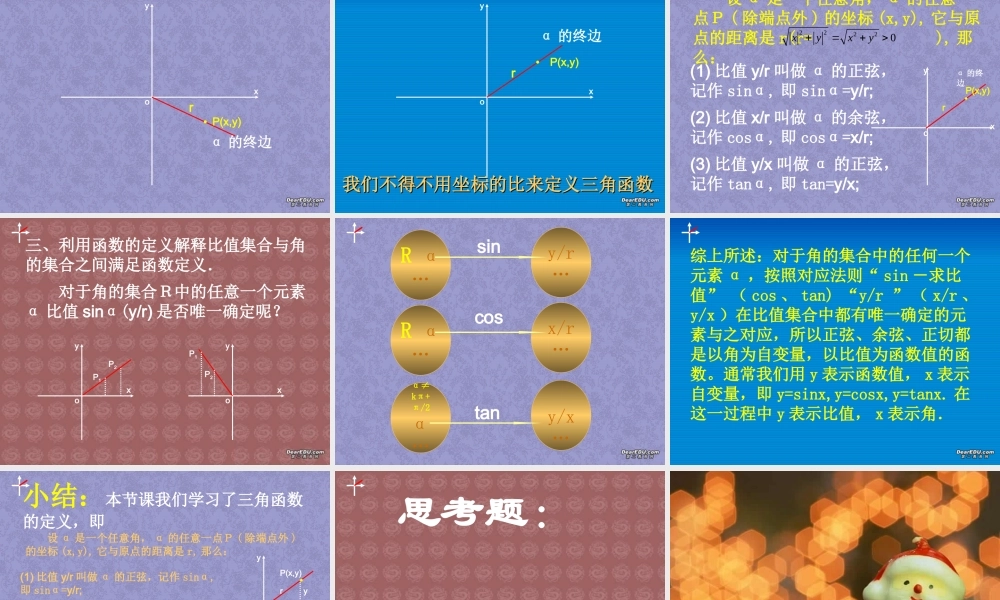
一、初中三角函数的定义：在直角三形 ABC 中，∠ A 是锐角，那么sin,cos,tan,cot.AAAAAAAAAA的对边的邻边斜边斜边的对边的邻边的邻边的对边ＡＢＣabcsin,cos,tan,cot.abAAabAAbacc( 图1) 前面我们已经将角的概念作出了推广 --- 任意角 .问题 : 那么对于任意角我们是否可以定义三角函数 ? 如果可以的话又怎样定义任意角的三角函数 ? 在角的概念的推广过程中，我们是将角放在直角坐标系中加以讨论的．我们为什么要将角放在直角坐标系中加以讨论呢？这样讨论能给我们带来什么样的好处呢？为此我们将锐角 ( 图 1) 放在直角坐标系中，看从中能够得到什么样的启示．oxyＡＢＣabcyx(x,y)sin,cos,tan,cot.AAAAAAAAAA的对边的邻边斜边斜边的对边的邻边的邻边的对边sin,cos,tan,cot.abAAabAAbaccsin,cos,tan,cot.yxAAyxAAxycc 上述过程向我们揭示了利用平面直角坐标系有可能完成任意角的三角函数的定义．即利用坐标的比来定义任意角的三角函数 . （这也是我们为什么要将任意角放在直角坐标系加以讨论的根本理由 . ）sin,cos,tan,cot.abAAabAAbaccsin,cos,tan,cot.yxAAyxAAxycc 二、任意角的三角函数的定义 .oxyP(x,y)rα 的终边oxyP(x,y)rα 的终边oxyP(x,y)rα 的终边oxyP(x,y)rα 的终边oxyP(x,y)rα 的终边oxyP(x,y)rα 的终边oxyP(x,y)rα 的终边oxyP(x,y)rα 的终边oxyP(x,y)rα 的终边oxyP(x,y)rα 的终边任意的三角函数的定义：我们不得不用坐标的比来定义三角函数我们不得不用坐标的比来定义三角函数 设 α 是一个任意角， α 的任意一点Ｐ ( 除端点外 ) 的坐标 (x,y), 它与原点的距离是 r(r= ), 那么： 22220xyxy(1) 比值 y/r 叫做 α 的正弦，记作 sinα, 即 sinα=y/r;(2) 比值 x/r 叫做 α 的余弦，记作 cosα, 即 cosα=x/r;(3) 比值 y/x 叫做 α 的正弦，记作 tanα, 即 tan=y/x;oxyP(x,y)rα 的终边三、利用函数的定义解释比值集合与角的集合之间满足函数定义． 对于角的集合Ｒ中的任意一个元素α 比值 sinα(y/r) 是否唯一确定呢？oxyP1P2oxyP2P1R α…x/r…R α…y/x…α≠kπ+π/2α…y/r…sincostan综上所述：对于角的集合中的任何一个元素 α ，按照对应法则“ sin －求比值” （ cos 、 tan) “y/r ” （ x/r 、y/x ）在比值集合中都有...