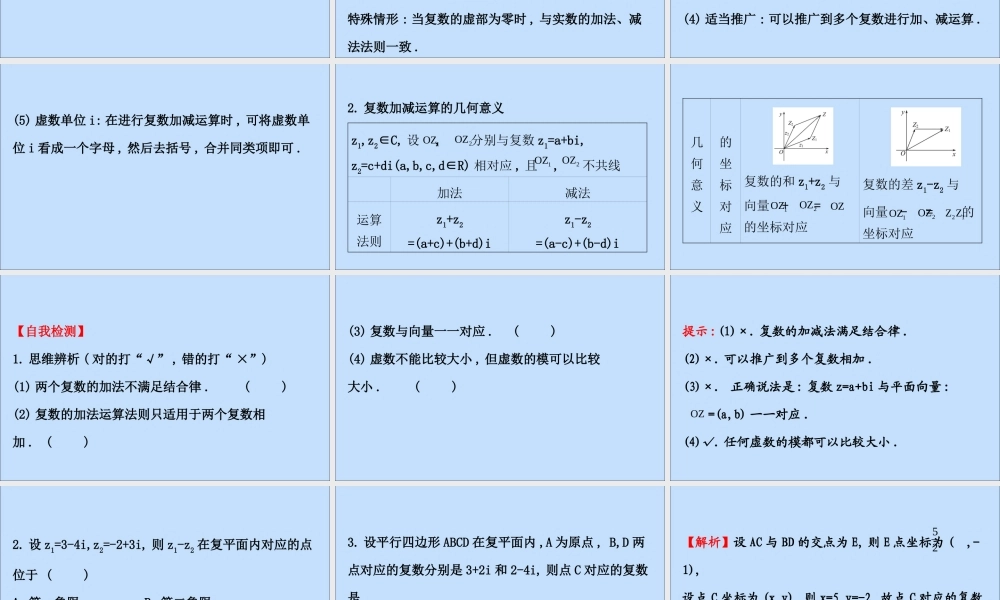
3.2 复数的运算3.2.1 复数的加法与减法【自我预习】1. 复数的加法、减法(1) 相反数 :a+bi 的相反数为 ______.-a-bi(2) 运算法则 :设 z1=a+bi,z2=c+di,a,b,c,d∈R.① 运算 z1+z2=_____________,z1-z2=_____________.② 法则 : 两个复数相加 ( 减 ) 就是把实部与实部、虚部与虚部分别 _________.(a+c)+(b+d)i(a-c)+(b-d)i相加( 减 )(3) 几何意义 :设复数 z1,z2 对应的向量分别为 , , 且 和 不共线 , 则复数 z1+z2 是以 OZ1,OZ2 为邻边的平行四边形 OZ1ZZ2 的 ________________________ 所对应的复数 ,z1-z2 是连接向量 和 的终点并指向________________ 所对应的复数 .1OZ�2OZ�1OZ�2OZ�对角线 OZ 所表示的向量 OZ�1OZ�2OZ� 的终点的向量1OZ�2. 复数加法的运算律(1) 交换律 :z1+z2=_____.(2) 结合律 :(z1+z2)+z3=__________.z2+z1z1+(z2+z3)【思考】(1) 两个复数的和是个什么数 , 它的值唯一确定吗 ?提示 : 仍然是个复数 , 是一个确定的复数 .(2) 若复数 z1,z2 满足 z1-z2>0, 能否认为 z1>z2?提示 : 不能 . 如 2+i-i>0, 但 2+i 与 i 不能比较大小 .【自我总结】1. 对复数的加减运算法则的五点说明(1) 一种规定 : 复数的加法法则是一种规定 , 减法是加法的逆运算 ;特殊情形 : 当复数的虚部为零时 , 与实数的加法、减法法则一致 .(2) 运算律 : 实数加法的交换律、结合律在复数集中仍成立 . 实数的移项法则在复数中仍然成立 .(3) 运算结果 : 两个复数的和 ( 差 ) 是唯一确定的复数 .(4) 适当推广 : 可以推广到多个复数进行加、减运算 .(5) 虚数单位 i: 在进行复数加减运算时 , 可将虚数单位 i 看成一个字母 , 然后去括号 , 合并同类项即可 .2. 复数加减运算的几何意义z1,z2∈C, 设, 分别与复数 z1=a+bi,z2=c+di(a,b,c,d∈R) 相对应 , 且, 不共线加法减法运算法则z1+z2=(a+c)+(b+d)iz1-z2=(a-c)+(b-d)i1OZ�2OZ�1OZ�2OZ�几何意义 的坐标对应复数的和 z1+z2 与 向量+ = 的坐标对应复数的差 z1-z2 与 向量- = 的坐标对应 1OZ�2OZ�OZ�1OZ�2OZ�21Z Z�【自我检测】1. 思维辨析 ( 对的打“√” , 错的打“ ×”)(1) 两个复数的加法不满足结合律 .( )(2) 复数的加法运算法则只适用于两个复数相加 .( )(3) 复数与向量一一对应 .( )(4) 虚数不能比较大小 , 但虚数的模可以...