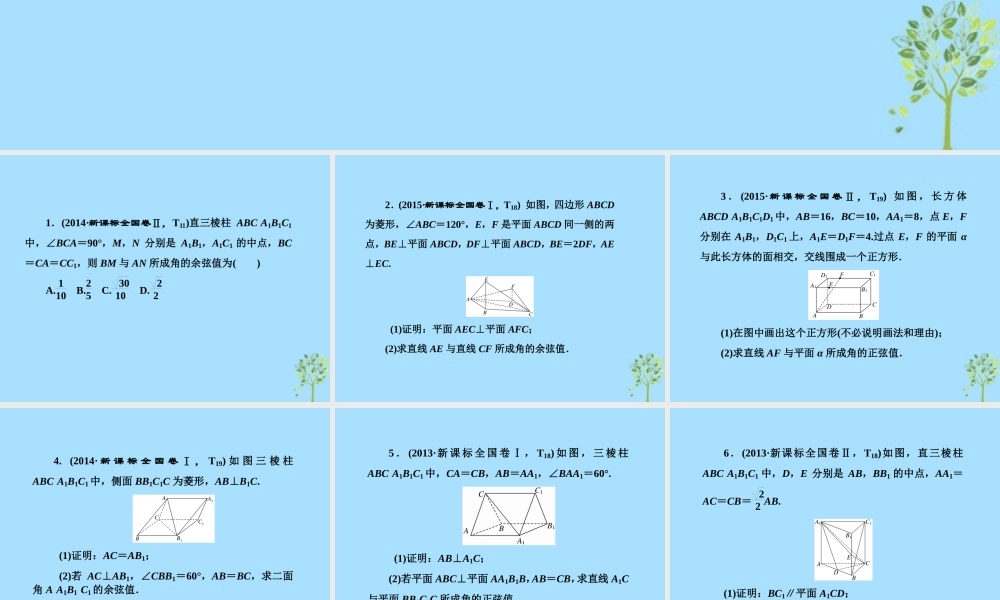
用向量解决立体几何角的问题用向量解决立体几何角的问题1.(2014·新课标全国卷Ⅱ,T11)直三棱柱 ABCA1B1C1中,∠BCA=90°,M,N 分别是 A1B1,A1C1 的中点,BC=CA=CC1,则 BM 与 AN 所成角的余弦值为( )A. 110 B.25 C. 3010 D. 22 2.(2015·新课标全国卷Ⅰ,T18) 如图,四边形 ABCD为菱形,∠ABC=120°,E,F 是平面 ABCD 同一侧的两点,BE⊥平面 ABCD,DF⊥平面 ABCD,BE=2DF,AE⊥EC. (1)证明:平面 AEC⊥平面 AFC;(2)求直线 AE 与直线 CF 所成角的余弦值. 3 . (2015·新 课 标 全 国 卷 Ⅱ , T19) 如 图 , 长 方 体ABCDA1B1C1D1 中,AB=16,BC=10,AA1=8,点 E,F分别在 A1B1,D1C1 上,A1E=D1F=4.过点 E,F 的平面 α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由);(2)求直线 AF 与平面 α 所成角的正弦值. 4. (2014· 新 课 标 全 国 卷 Ⅰ , T19) 如 图 三 棱 柱ABCA1B1C1 中,侧面 BB1C1C 为菱形,AB⊥B1C. (1)证明:AC=AB1;(2)若 AC⊥AB1,∠CBB1=60°,AB=BC,求二面角 AA1B1C1 的余弦值. 5 . (2013·新 课 标 全 国 卷 Ⅰ , T18) 如 图 , 三 棱 柱ABCA1B1C1 中,CA=CB,AB=AA1,∠BAA1=60°. (1)证明:AB⊥A1C;(2)若平面 ABC⊥平面 AA1B1B,AB=CB,求直线 A1C与平面 BB1C1C 所成角的正弦值. 6.(2013·新课标全国卷Ⅱ,T18)如图,直三棱柱ABCA1B1C1 中,D,E 分别是 AB,BB1 的中点,AA1=AC=CB= 22 AB. (1)证明:BC1∥平面 A1CD;(2)求二面角 DA1CE 的正弦值. 7 . (2012·新 课 标 全 国 卷 , T19) 如 图 , 直 三 棱 柱ABCA1B1C1 中,AC=BC=12AA1,D 是棱 AA1 的中点,DC1⊥BD. (1)证明:DC1⊥BC;(2)求二面角 A1BDC1 的大小. 8.(2011·课标全国卷,T18)如图,四棱锥 PABCD 中,底面 ABCD 为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面 ABCD.(1)证明:PA⊥BD;(2)若 PD=AD,求二面角 APBC 的余弦值. 1.向量法求异面直线所成的角 若异面直线 a,b 的方向向量分别为 a,b,异面直线所成的角为 θ,则 cos θ=|cos〈a,b〉|=|a·b||a||b|...