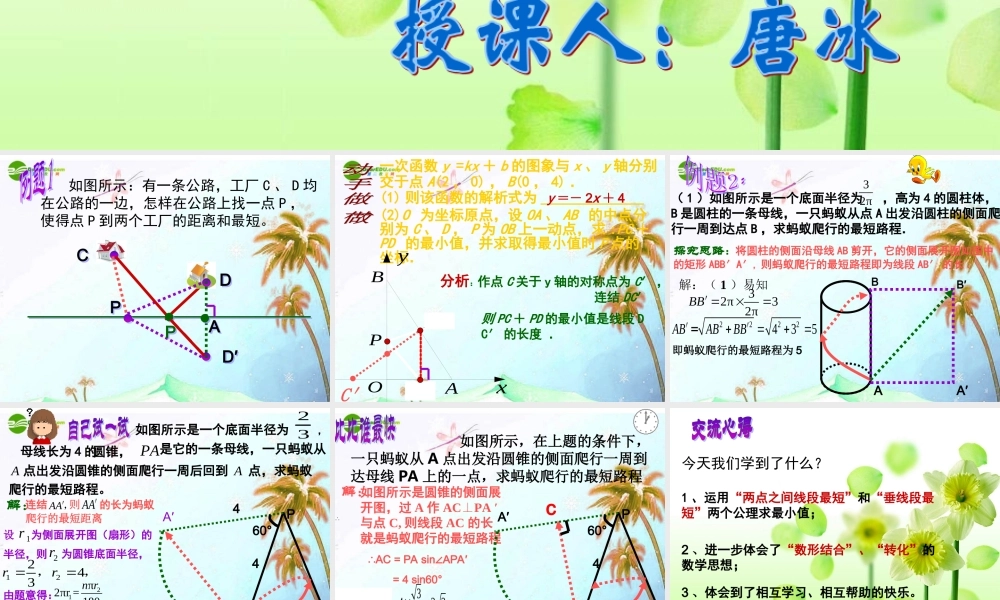
如图所示:有一条公路,工厂 C 、 D 均在公路的一边,怎样在公路上找一点 P ,使得点 P 到两个工厂的距离和最短。CCDDPPD′D′PPAA 一次函数 y =kx + b 的图象与 x 、 y 轴分别交于点 A(2 , 0) , B(0 , 4) .(1) 则该函数的解析式为 ______________(2)O 为坐标原点,设 OA 、 AB 的中点分别为 C 、 D , P 为 OB 上一动点,求 :PC +PD 的最小值,并求取得最小值时 P 点的坐标.OxyBDACPy =- 2x + 4 C′分析:作点 C 关于 y 轴的对称点为 C′ , 连结 DC′则 PC + PD 的最小值是线段 DC′ 的长度 . ( 1 )如图所示是一个底面半径为 ,高为 4 的圆柱体, AB 是圆柱的一条母线,一只蚂蚁从点 A 出发沿圆柱的侧面爬行一周到达点 B ,求蚂蚁爬行的最短路程.32π探究思路:将圆柱的侧面沿母线 AB 剪开,它的侧面展开图如图中的矩形 ABB′A′, 则蚂蚁爬行的最短路程即为线段 AB′ 的长 .ABB′A′解:( 1 )易知32π32πBB ′ 2222435ABABBB′=′即蚂蚁爬行的最短路程为 5 23PAAA如图所示是一个底面半径为 , 母线长为 4 的是它的一条母线,一只蚂蚁从点出发沿圆锥的侧面爬行一周后回到点,求蚂蚁圆锥,爬行的最短路程。APAA′, AA′1r2r12243rr,,21π2πr = 180n r连结则为圆锥底面半径,为侧面展开图(扇形)的由题意得:的长为蚂蚁A′半径,则22ππ43180n 即 60nPAA△′是等边三角形 4AAPA′.∴ 最短路程为 设·460° 4解:爬行的最短距离° 如图所示,在上题的条件下,一只蚂蚁从 A 点出发沿圆锥的侧面爬行一周到达母线 PA 上的一点,求蚂蚁爬行的最短路程 如图所示是圆锥的侧面展开图,过 A 作 ACPA ′⊥与点 C, 则线段 AC 的长就是蚂蚁爬行的最短路程2 3.∴ 蚂蚁爬行的最短距离为 APA′·460° c∴AC = PA sin APA′∠= 4 sin60°3sin4 sin6042 32ACPAAPA °解: 今天我们学到了什么?1 、运用“两点之间线段最短”和“垂线段最短”两个公理求最小值;2 、进一步体会了“数形结合”、“转化”的数学思想;3 、体会到了相互学习、相互帮助的快乐。 xyO2113424yxx( 2 )有一动点 Q 在线段 AB上运动,△ QCD 的周长在不断变化时是否存在最小值?若存在,求点 Q 的坐标;若不存在,说明理由.QC′如图,设抛物线 交 x 轴于 A 、 B 两点,顶点为 D .以 AB 为直径作半圆M ,半圆交 y 轴负半轴于 C . ( 1 )求抛物线的对称轴;Q