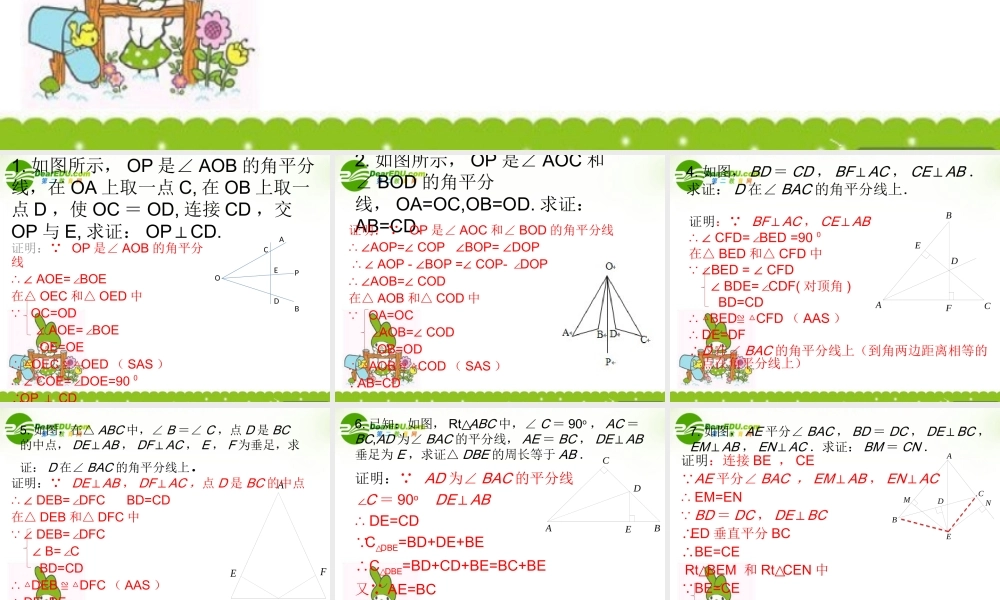
角平分线练习课1. 如图所示, OP 是∠ AOB 的角平分线,在 OA 上取一点 C, 在 OB 上取一点 D ,使 OC = OD, 连接 CD ,交OP 与 E, 求证: OP⊥CD.证明:∵ OP 是∠ AOB 的角平分线 ∴ ∠ AOE=∠BOE在△ OEC 和△ OED 中 ∵OC=OD ∠ AOE=∠BOE OE=OE ∴ △OEC ≌ △OED ( SAS ) ∴ ∠ COE=∠DOE=90 0∴OP CD⊥ABOPCDE2. 如图所示, OP 是∠ AOC 和∠ BOD 的角平分线, OA=OC,OB=OD. 求证:AB=CD.证明:∵ OP 是∠ AOC 和∠ BOD 的角平分线 ∴ ∠AOP= ∠ COP ∠BOP= ∠DOP ∴ ∠ AOP - ∠BOP = ∠ COP- ∠DOP ∴ ∠AOB= ∠ COD 在△ AOB 和△ COD 中 ∵OA=OC ∠AOB= ∠ COD OB=OD ∴ △AOB ≌ △COD ( SAS )∴AB=CDFEDCBA4. 如图, BD = CD , BF⊥AC , CE⊥AB .求证: D 在∠ BAC 的角平分线上.证明:∵ BF⊥AC , CE⊥AB ∴ ∠ CFD=∠BED =90 0在△ BED 和△ CFD 中 ∵ ∠BED = ∠ CFD ∠ BDE=∠CDF( 对顶角 ) BD=CD ∴ △BED ≌ △CFD ( AAS ) ∴ DE=DF∴ D 在∠ BAC 的角平分线上(到角两边距离相等的点在角平分线上)FEDCBA5. 如图,在△ ABC 中,∠ B =∠ C ,点 D 是 BC的中点, DE⊥AB , DF⊥AC , E , F 为垂足,求证: D 在∠ BAC 的角平分线上.证明:∵ DE⊥AB , DF⊥AC ,点 D 是 BC 的中点 ∴ ∠ DEB=∠DFC BD=CD在△ DEB 和△ DFC 中 ∵ ∠ DEB=∠DFC ∠ B=∠C BD=CD ∴ △DEB ≌ △DFC ( AAS ) ∴ DE=DF∴ D 在∠ BAC 的角平分线上(到角两边距离相等的点在角平分线上)ABCDE6. 已知:如图, Rt△ABC 中,∠ C = 90o , AC =BC,AD 为∠ BAC 的平分线, AE = BC , DE⊥AB垂足为 E ,求证△ DBE 的周长等于 AB .证明:∵ AD 为∠ BAC 的平分线∠C = 90o DE⊥AB ∴ DE=CD∵C△DBE=BD+DE+BE∴ C△DBE=BD+CD+BE=BC+BE又∵ AE=BC∴ C△DBE=BC+BE=AE+BE=AB即△ DBE 的周长等于 ABNMEDCBA7. 如图, AE 平分∠ BAC , BD = DC , DE⊥BC ,EM⊥AB , EN⊥AC .求证: BM = CN .证明:连接 BE , CE∵ AE 平分∠ BAC , EM⊥AB , EN⊥AC ∴ EM=EN ∵ BD = DC , DE⊥BC∴ED 垂直平分 BC∴ BE=CE Rt△BEM 和 Rt△CEN 中∵ BE=CE EM=EN ∴ △BEM ≌ △CEN ( HL ) ∴ BM=CNABCDFNPM9. 已知:如图, PA 、 PC 分别是△ ABC 外角∠ MAC 与∠ NCA 的平分线,它们交于P , PD⊥BM 于 M , PF⊥BN 于 F .求证: BP 为∠ MBN 的平分线证明:作 PQ ⊥AC 于 Q∵ PA 平分∠ MAC , PC 平分∠ NCA ∴ PD=PQ , PF=PQ∴PD=PF∵ PD⊥BM , PF⊥BN∴ 点 P 在 ∠ MBN 的平分线上即 BP 为∠ MBN 的平分线Q