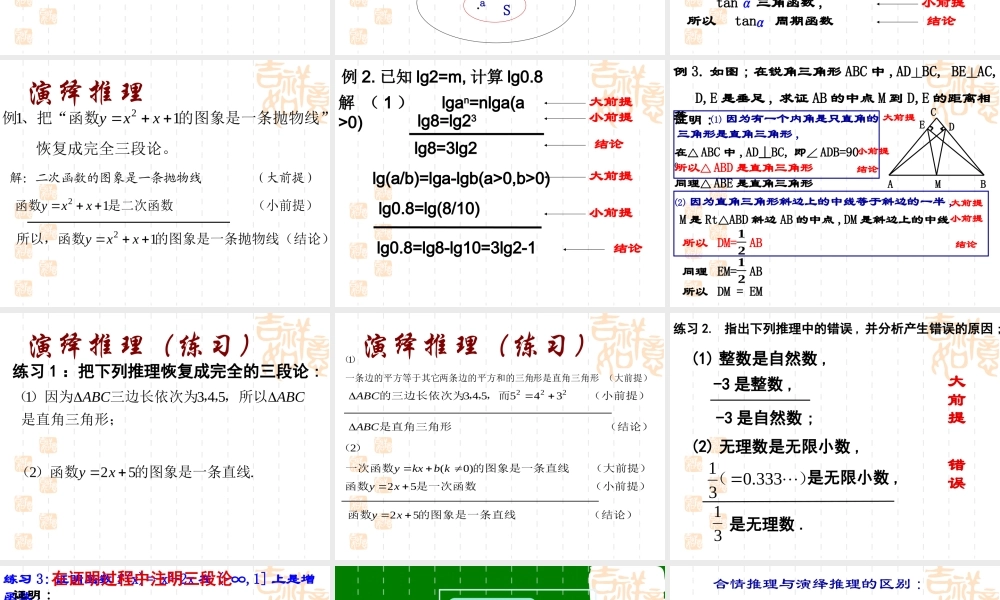
复习 : 合情推理 归纳推理 从特殊到一般 类比推理 从特殊到特殊从具体问题出发观察、分析比较、联想提出猜想归纳类比 观察与是思考1. 所有的金属都能导电 , 2. 一切奇数都不能被 2 整除 , 3. 三角函数都是周期函数 , 铜能够导电 .铜是金属 , (2100+1) 不能被 2 整除 .(2100+1) 是奇数 , tan 周期函数 tan 三角函数 ,是合情推理吗? 从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为演绎推理.注:1.演绎推理是由一般到特殊的推理;2.“三段论”是演绎推理的一般模式;包括 ⑴大前提 --- 已知的一般原理; ⑵小前提 --- 所研究的特殊情况; ⑶结论 ----- 据一般原理,对特殊情况做出的判断. 演绎推理 三段论的基本格式M—P ( M 是P )S—M ( S 是M )S—P ( S 是P )(大前提)(小前提)(结论) 3. 三段论推理的依据 , 用集合的观点来理解 :若集合 M 的所有元素都具有性质 P,S 是 M 的一个子集 , 那么 S 中所有元素也都具有性质P.MSa注: 观察与是思考 1. 所有的金属都能导电 , 2. 一切奇数都不能被 2 整除 , 3. 三角函数都是周期函数 , 所以,铜能够导电 .铜是金属 , 所以, (2100+1) 不能被 2 整除 .(2100+1) 是奇数 ,所以 tan 周期函数 tan 三角函数 ,大前提小前提结论大前提小前提结论结论小前提大前提 演绎推理恢复成完全三段论。的图象是一条抛物线”、把“函数例112xxy解:二次函数的图象是一条抛物线 (大前提)(小前提)是二次函数函数12xxy结论)的图象是一条抛物线(所以,函数12xxy 例 2. 已知 lg2=m, 计算 lg0.8解 ( 1 ) lgan=nlga(a>0)lg8=lg23lg8=3lg2 lg(a/b)=lga-lgb(a>0,b>0)lg0.8=lg(8/10)lg0.8=lg8-lg10=3lg2-1大前提小前提结论大前提小前提结论 例 3. 如图 ; 在锐角三角形 ABC 中 ,AD⊥BC, BE⊥AC, D,E 是垂足 , 求证 AB 的中点 M 到 D,E 的距离相等 .ADECMB (1) 因为有一个内角是只直角的三角形是直角三角形 ,在△ ABC 中 ,AD⊥BC, 即∠ ADB=900所以△ ABD 是直角三角形同理△ ABE 是直角三角形(2) 因为直角三角形斜边上的中线等于斜边的一半 ,M 是 Rt△ABD 斜边 AB 的中点 ,DM 是斜边上的中线所以 DM= AB12同理 EM= AB12所以 DM = EM大前提小前提结论大前提小前提结论证明 : 演绎推理(练...