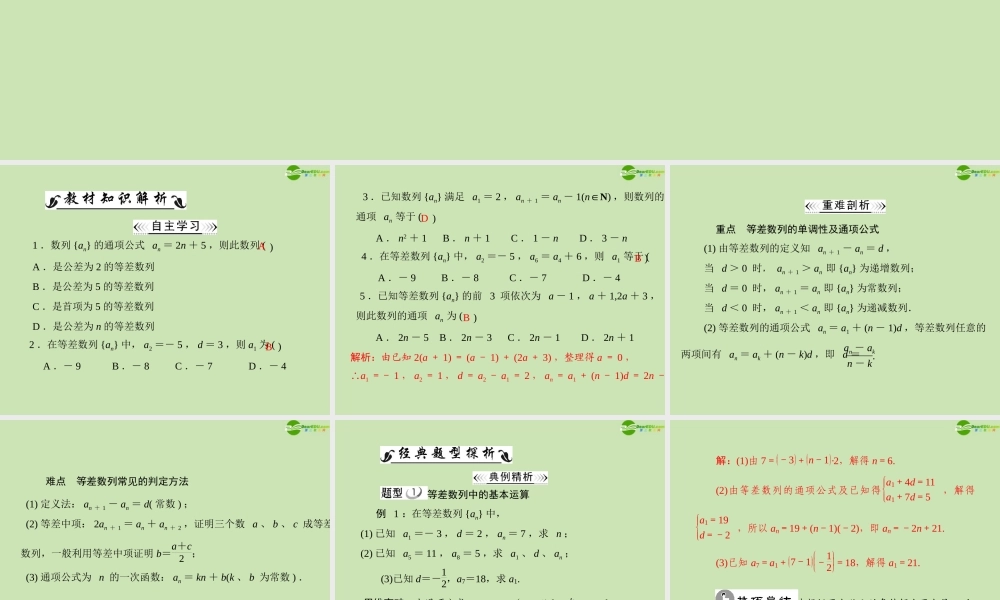
2 . 2 等差数列2 . 2.1 等差数列的定义及通项公式)1 .数列 {an} 的通项公式 an = 2n + 5 ,则此数列 (A .是公差为 2 的等差数列B .是公差为 5 的等差数列C .是首项为 5 的等差数列D .是公差为 n 的等差数列2 .在等差数列 {an} 中, a2 =- 5 , d = 3 ,则 a1 为 ( )BA .- 9B .- 8C .- 7D .- 4 A3 .已知数列 {an} 满足 a1 = 2 , an + 1 = an - 1(n∈N) ,则数列的通项 an 等于 ()DA . n2 + 1B . n + 1C . 1 - nD . 3 - n4 .在等差数列 {an} 中, a2 =- 5 , a6 = a4 + 6 ,则 a1 等于 ()A .- 9B .- 8C .- 7D .- 4B5 .已知等差数列 {an} 的前 3 项依次为 a - 1 , a + 1,2a + 3 ,则此数列的通项 an 为 ()BA . 2n - 5B . 2n - 3C . 2n - 1D . 2n + 1解析:由已知 2(a + 1) = (a - 1) + (2a + 3) ,整理得 a = 0 ,∴a1 =- 1 , a2 = 1 , d = a2 - a1 = 2 , an = a1 + (n - 1)d = 2n - 3.重点等差数列的单调性及通项公式(1) 由等差数列的定义知 an + 1 - an = d ,当 d > 0 时, an + 1 > an 即 {an} 为递增数列;当 d = 0 时, an + 1 = an 即 {an} 为常数列;当 d < 0 时, an + 1 < an 即 {an} 为递减数列.(2) 等差数列的通项公式 an = a1 + (n - 1)d ,等差数列任意的两项间有 an = ak + (n - k)d ,即 d =an - akn - k.难点等差数列常见的判定方法(1) 定义法: an + 1 - an = d( 常数 ) ;(2) 等差中项: 2an + 1 = an + an + 2 ,证明三个数 a 、 b 、 c 成等差(3) 通项公式为 n 的一次函数: an = kn + b(k 、 b 为常数 ) .数列,一般利用等差中项证明 b=a+c2 ; 等差数列中的基本运算例 1 :在等差数列 {an} 中,(1) 已知 a1 =- 3 , d = 2 , an = 7 ,求 n ;(2) 已知 a5 = 11 , a8 = 5 ,求 a1 、 d 、 an ;思维突破:由通项公式 an = a1 + (n - 1)d ,在 a1 、 d 、 n 、 an四个量中,可由其中任意三个量求第四个量.(3)已知 d=-...