新课标高一数学向量的加法课件0 课件VIP免费

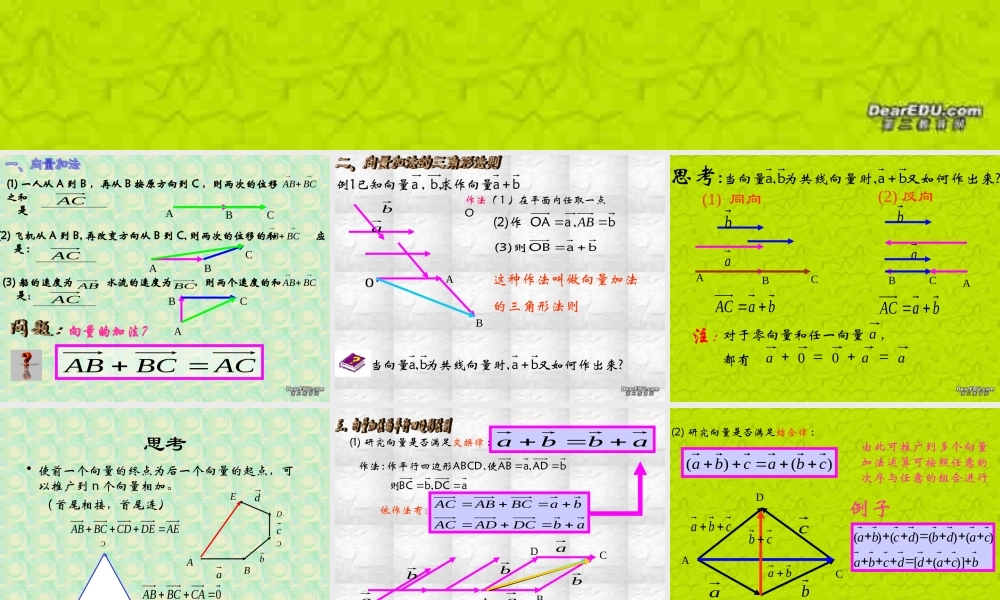
1. 三角形法则 2. 平行四边形法则  BCABABCAC (2) 飞机从 A 到 B, 再改变方向从 B 到 C, 则两次的位移的和 应 是 : BCABABCAC(3) 船的速度为 ，水流的速度为 ，则两个速度的和 是：ABBCABCAC 向量的加法？ACBCAB(1) 一人从 A 到 B ，再从 B 按原方向到 C ，则两次的位移之和 是 BCABba求作向量b, , a 例1已知向量ab作法（ 1 ）在平面内任取一点Oo·b, aOA (2)作ABbaOB (3)则AB这种作法叫做向量加法的三角形法则又如何作出来?ba为共线向量时,b,a当向量(1) 同向(2) 反向baACbaAC又如何作出来?ba为共线向量时,b,a当向量:思考abABCabABC注：a0aa 0,都有对于零向量和任一向量a 思考• 使前一个向量的终点为后一个向量的起点，可以推广到 n 个向量相加。 ( 首尾相接，首尾连）abcdAEBCDAEDECDBCABABC0CABCAB(1) 研究向量是否满足交换律 :abbaabbAD,aAB使,作平行四边形ABCD:作法ABDaDC,bBC则Caabb依作法有：abDCADACbaBCABAC(2) 研究向量是否满足结合律 :)()(cbacbaCBAcbaba cb abcD由此可推广到多个向量加法运算可按照任意的次序与任意的组合进行bcaddcbacadbdcba)]([)()()()(例子 流速间的夹角表示）大小和方向。（用与水，求船实际航行速度的hkm的流速为2的方向行驶，同时河水的速度向垂直于对岸hkm3A点出发以2例2：如图，一艘船从。就是船实际航行的速度ACABCD，则四边形D、AB为邻边作平行表示水流的速度，以AAB驶的速度表示船向垂直于对岸行AD解：如图，设32|BC|2，|AB| 在Rt△ABC中,ABDC4|AC||AD||AB|2260CAB答：船实际航行速度大小为 4km/h ，方向与流速间的夹角为 60 。（ 1 ）abbba ababa （ 2）（ 4）abba b四、课堂练习一、用三角形法则求向量的和a（ 2 ）bbba 二、用平行四边形法则求向量的和bcdaabcdABCDO三、看图填写DACB 四、根据图示填空：a+b=c+d=a+b+d=c+d+e=ACADAEADabcdABCDEgfe课堂练习 3. 一艘船以 5km/h 的速度在行驶，同时河水的流速为 2km/h ，则船的实际航行速度大小最大是 ，最小是 。 COBOOCOA化简.2BAhkm/7hkm/3为，则飞机两次位移的和南飞行，然后改变方向向一架飞机向西飞行kmkm100100.1km2100向西南方向飞行课堂训练1 、如图， ABC 中 O 为重心， D 、 E 、 F 分别是 BC 、AC 、 AB 的中点，化简下列三式：(1) BC+CE+EA=(2) OE+AB+EA=(3) AB+FE+DC=2 、用向量方法证明： 对角线互相平分的四边形是平行四边形。ABCDoEF )cb(ac)ba(abba作业： P104 3 、 4 、 5