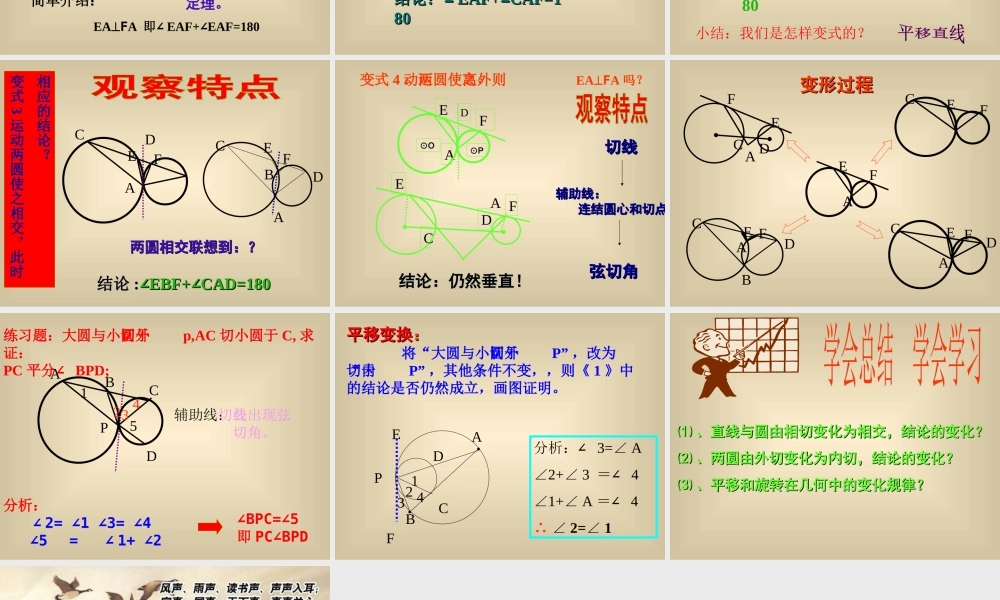
《圆与圆的位置关系》《圆与圆的位置关系》专题复习专题复习 《圆与圆的位置关系》专题复习《圆与圆的位置关系》专题复习 由此基本图形,我由此基本图形,我们能想到哪些知识们能想到哪些知识点点 :__________________.:__________________..p.oAB⑴ 、直角三角形⑵ 、弦切角⑶ 、两圆相切的 辅助线的做法。 公切线弦切角公共弦圆内接四边形外角 已知:如图,⊙已知:如图,⊙ oo 和和⊙⊙ pp 外切于点外切于点 AA ,, EFEF 是两圆是两圆的公切线,的公切线, EE 、、 FF 为切点。为切点。求证:求证: EAEAFFAA 。。 辅助线:做公切线知识点:1 、切线长定理。2 、直角三角形的判定 定理。简单介绍: EAFA 即∠ EAF+∠EAF=180 AEFD⊙O⊙P 变式 1 :拖动直线,使其变化为⊙ P的切线和割线 , 上述结论有何变化?结论:结论:∠∠ EAF+EAF+∠∠CAF=1CAF=18080 AEFCDAEFD⊙O⊙P 变式 2 :继续拖动直线使之成为两圆割线,如图,则类似上题结论?结论:∠ EAD+∠CAF=180小结:我们是怎样变式的?AEFCDAEFCD学法指导:类比 相应的结论?变式3运动两圆使之相交,此时结论结论 ::∠∠EBF+EBF+∠∠CAD=180CAD=180两圆相交联想到:?两圆相交联想到:?CDBFAEAEFCD 变式 4 :运动两圆使之外离,则 EAFA 吗?结论:仍然垂直!结论:仍然垂直!切线切线辅助线:辅助线: 连结圆心和切点连结圆心和切点弦切角弦切角A FCDEAEFD⊙O⊙P 变形过程变形过程AEFEFCAE FCDDBCE FAAFECD 练习题:大圆与小圆外切于p,AC 切小圆于 C, 求证:PC 平分∠ BPD;辅助线:公切线出现弦 切角。PBCAD213 45分析: ∠ 2= ∠1 ∠3= ∠4 ∠5 = ∠ 1+ ∠2∠BPC=∠5 即 PC∠BPD 平移变换平移变换:: 将“大圆与小圆外切于P” ,改为“内切于P” ,其他条件不变,,则《 1 》中的结论是否仍然成立,画图证明。AE3CBDP12F4分析:∠ 3=∠ A∠2+∠ 3 =∠ 4∠1+∠ A =∠ 4 ∴ ∠ 2=∠ 1 ⑴⑴ 、直线与圆由相切变化为相交,结论的变化?、直线与圆由相切变化为相交,结论的变化?⑵⑵ 、两圆由外切变化为内切,结论的变化?、两圆由外切变化为内切,结论的变化?⑶⑶ 、平移和旋转在几何中的变化规律?、平移和旋转在几何中的变化规律?