九年级数学下册 281 锐角三角函数(第2课时)课件1 (新版)新人教版 课件VIP免费

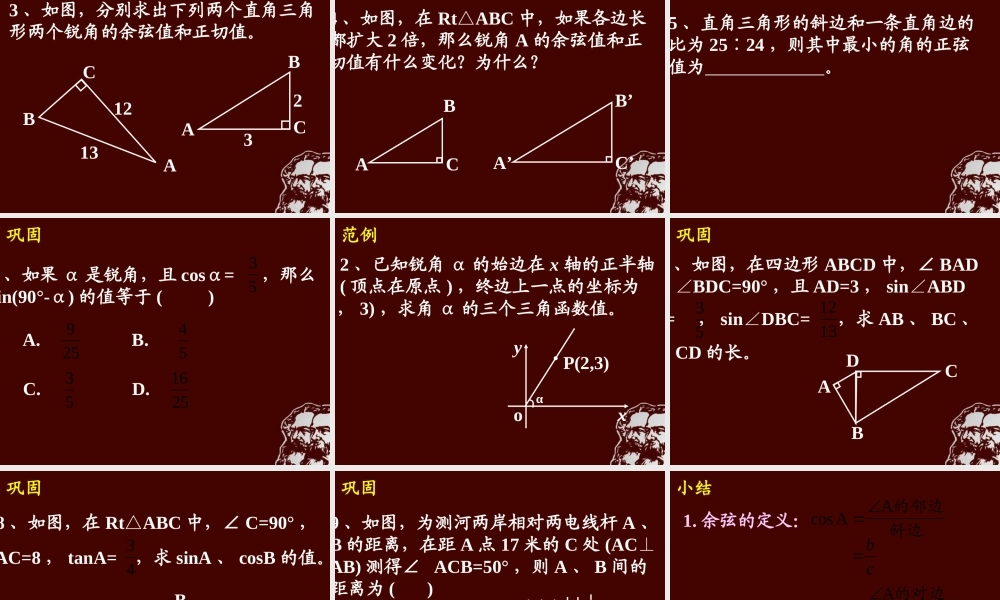
锐角三角函数 (2) 锐角三角函数 (2) 复习1 、如图，分别求出下列两个直角三角形两个锐角的正弦值。ACBACB131232复习2 、如图，在 RtABC△中，∠ C=90° 。(1) 如果 A 的度数一定，则 是一个固定值；(2) 什么叫做正弦？ACB复习 在直角三角形中，当锐角 A 的度数一定时，不管三角形的大小如何，∠ A的对边与斜边的比都的一个固定值。直角三角形的性质：复习正弦的定义： 在 RtABC△中，∠ C=90° ，我们把锐角 A 的对边与斜边的比叫做∠ A 的正弦。记作 sinA ，即斜边的对边AAsinca探究一、如图，在 RtABC△中，∠ C=90° 。ACB对边 a邻边 b斜边 c 当∠ A 确定时，∠ A 的对边与斜边的比就确定，此时，其他边之间的比是否也确定呢？探究二、如图， RtABC△和 RtA’B’C’△中，∠C=C’=90°∠，∠ A=A’=∠α ，那么ACBACB与 有什么关系？ABACBACAα探究三、如图，在 RtABC△中，∠ C=90° 。ACB对边 a邻边 b斜边 c 当∠ A 确定时，∠ A 的对边与斜边的比就确定，此时，其他边之间的比是否也是确定的。新授如图，在 RtABC△中，∠ C=90° 。ACB斜边的邻边AAcoscb对边 a邻边 b斜边 c的邻边的对边AAAtanab归纳余弦的定义： 在 RtABC△中，∠ C=90° ，我们把锐角 A 的邻边与斜边的比叫做∠ A 的余弦。记作 cosA ，即斜边的邻边AAcoscb归纳正切的定义： 在 RtABC△中，∠ C=90° ，我们把锐角 A 的对边与邻边的比叫做∠ A 的正切。记作 tanA ，即的邻边的对边AAAtanba归纳三角函数的定义： 锐角 A 的正弦、余弦、正切都叫做锐角三角函数。范例例 1 、如图，在 RtABC△中，∠ C=90° ，ACB653BC=6 ， sinA= ，求 cosA 、 tanB 的值。巩固3 、如图，分别求出下列两个直角三角形两个锐角的余弦值和正切值。ACBACB131232巩固4 、如图，在 RtABC△中，如果各边长都扩大 2 倍，那么锐角 A 的余弦值和正切值有什么变化？为什么？ACBA’C’B’巩固5 、直角三角形的斜边和一条直角边的比为 2524∶，则其中最小的角的正弦值为 。巩固6 、如果 α 是锐角，且 cosα= ，那么sin(90°-α) 的值等于 ( ) 53A. B.C. D.25954532516范例例 2 、已知锐角 α 的始边在 x 轴的正半轴上 ( 顶点在原点 ) ，终边上一点的坐标为(2 ， 3) ，求角 α 的三个三角函数值。xoyP(2,3)α巩固7 、如...