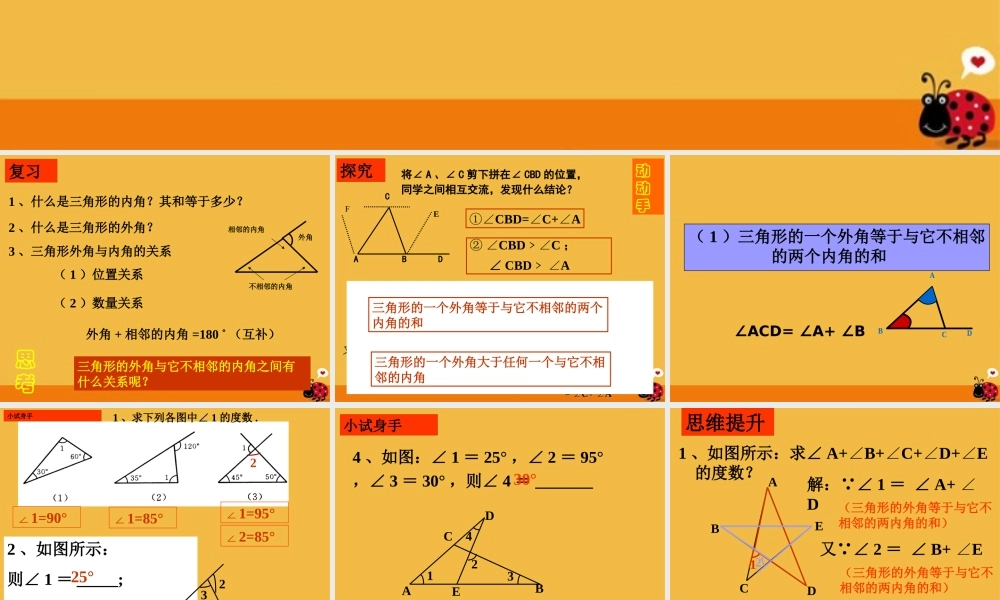
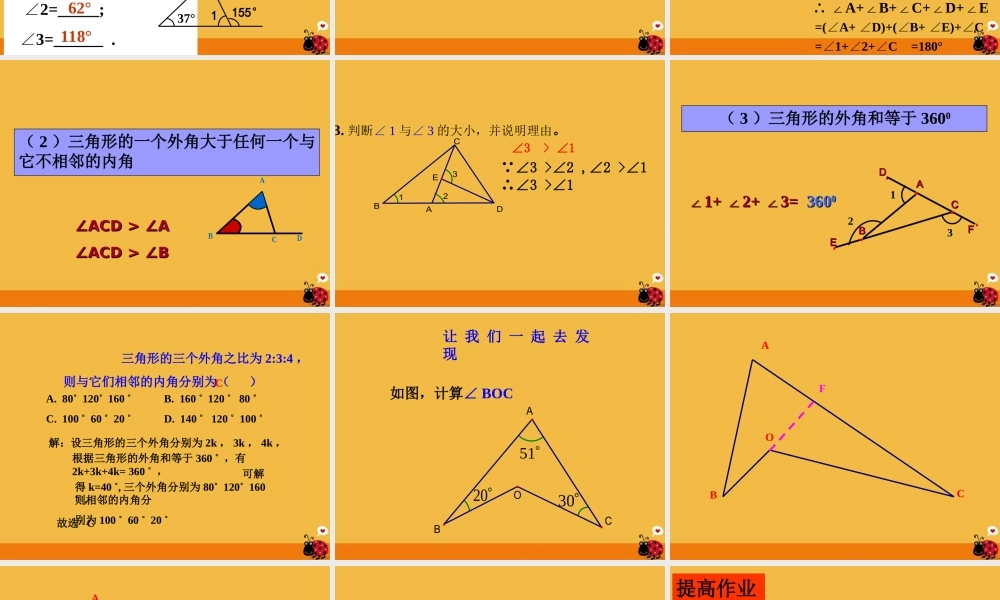
9.1 三角形(第 3 课时)三角形的外角和华东师大版七年级(下册)外角3 、三角形外角与内角的关系( 1 )位置关系( 2 )数量关系外角 + 相邻的内角 =180 ˚ (互补)相邻的内角不相邻的内角1 、什么是三角形的内角?其和等于多少?复习2 、什么是三角形的外角?思考三角形的外角与它不相邻的内角之间有什么关系呢?探究ADCB①∠CBD=C+A∠∠将∠ A 、∠ C 剪下拼在∠ CBD 的位置,同学之间相互交流,发现什么结论?动动手E ∠ABC + CBD= ∠180 °又 ∠ ABC+ C+ A= ∠∠180 ° ∴ ∠CBD= C+ A∠∠证明(一)证明(二):过过 BB 点作 点作 BEBE∥∥ACAC ∴ ∠ ∴ ∠EBD = A ( ∠EBD = A ( ∠?? ) )∠∠CBE = C ( ∠CBE = C ( ∠? ? )) ∴ ∠ ∴ ∠CBD = CBE+ EBD∠∠CBD = CBE+ EBD∠∠= C+ A∠∠= C+ A∠∠F ② ∠CBD﹥C∠; ∠ CBD ﹥A∠三角形的一个外角等于与它不相邻的两个内角的和三角形的一个外角大于任何一个与它不相邻的内角 ( 1 )三角形的一个外角等于与它不相邻 的两个内角的和ABCD∠ACD= ∠A+ ∠B1 、求下列各图中∠ 1 的度数 .小试身手2∠1=90°∠1=85°∠1=95°∠2=85°2 、如图所示:则∠ 1 = _____; ∠2=_____; ∠3=______ . 2155°37°3125°62°118°小试身手4 、如图:∠ 1 = 25° ,∠ 2 = 95°,∠ 3 = 30° ,则∠ 4 = _______ADECB143230°思维提升1 、如图所示:求∠ A+B+C+D+E∠∠∠∠ 的度数?EDCBA12解: ∠ 1 = ∠ A+ ∠D(三角形的外角等于与它不相邻的两内角的和)又 ∠ 2 = ∠ B+ E∠(三角形的外角等于与它不相邻的两内角的和) ∴ ∠A+B+C+D+E∠∠∠∠=(A+ D)+(B+ E)+C∠∠∠∠∠=1+2+C∠∠∠=180°( 2 )三角形的一个外角大于任何一个与它不相邻的内角ABCD∠∠ACD > ∠AACD > ∠A∠∠ACD > ∠BACD > ∠B3. 判断∠ 1 与∠ 3 的大小,并说明理由。321CBADE ∠3 >∠2 ,∠2 >∠1∴∠3 >∠1∠3 > ∠1( 3 )三角形的外角和等于 3600DDEEFFAACCBB112233∠∠1+ 2+ 3= ∠∠1+ 2+ 3= ∠∠36036000 三角形的三个外角之比为 2:3:4 , 则与它们相邻的内角分别为( ) A. 80˚ 120˚ 160 ˚ B. 160 ˚ 120 ˚ 80 ˚ C. 100 ˚ 60 ˚ 20 ˚ D. 140 ˚ 120 ˚ 100 ˚ 解:设三角形的三个外角分别为...