函数型综合问题三 北师大版 课件VIP免费

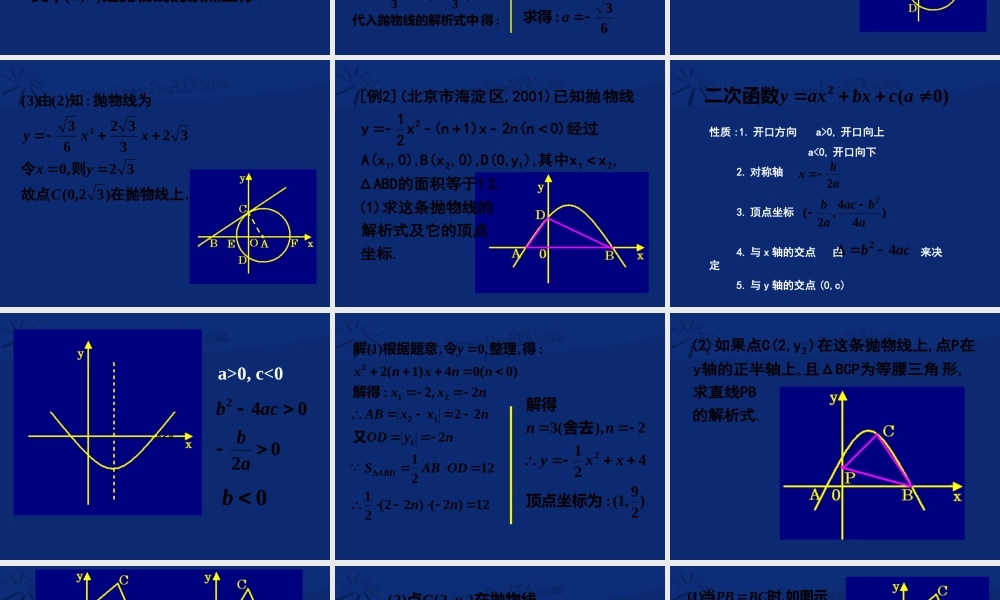
函数型综合问题三函数型综合问题三)0(2acbxaxy.,)3(.,,)2()1(.,,,),0,2(,4,,)2000,](1[2并说明理由是否在抛物线上试判断点求抛物线的解析式轴的交点与轴的交点恰为圆与上的顶点在直线若抛物线的解析式求直线于轴交的切线点作圆过两点轴交于与两点轴交于与点的坐标为的半径为圆角坐标系中在直如图西安市例CxAxBCcbxaxyBCBxBCACDCyFExAAACBCABCCAOACOCOAACOCAOCRtACOAAC相切与圆且即中在由题知连结解6030)32,0(32,4,2,)1(22)0,6(8230,BACABBABCRt中在则有为设直线bkxyBC3233333206xyBCkbbk的解析式为直线.),()0()(.3.)0,(),0,()0)()((.2)0(.1221212是抛物线的顶点坐标其中两个交点的坐标轴的是抛物线与其中khakhxayxxxaxxxxayacbxaxy:)338,2(338,22623233),()6)(2()0,6(),0,2(:)2(得代入抛物线的解析式中即而上在直线又其顶点故设抛物线的解析为由题知PnmxynmPxxayFE63:)62)(22(338aa求得3233263:)6)(2(632xxyxxy即抛物线的解析式为.)32,0(32,03233263:)2()3(2在抛物线上故点则令抛物线为知由Cyxxxy坐标.解析式及它的顶点(1)求这条抛物线的2.ΔABD的面积等于1,x其中x),yD(0,,0),B(x,0),A(x0)经过2n(n1)x(nx21y物线区,2001)已知抛[例2](北京市海淀211212)0(2acbxaxy二次函数性质 :1. 开口方向 a>0, 开口向上 a<0, 开口向下 2. 对称轴 3. 顶点坐标 4. 与 x 轴的交点 由 来决定 5. 与 y 轴的交点 (0,c)abx2)44,2(2abacabacb42 a>0, c<002042abacb0b0b12)2()22(2112212222,2:)0(04)1(2:,,0,)1(112212nnODABSnyODnxxABnxxnnxnxyABD又解得得整理令根据题意解)29,1(:4212),(32顶点坐标为舍去解得xxynn的解析式.求直线PB形,且ΔBCP为等腰三角y轴的正半轴上,点P在)在这条抛物线上,y(2)如果点C(2,252)24(4)4,0(),0,4(),0,2(:)4,2(442221421),2()2(222222BCDBACyxxyyC又据题意知上在抛物线点2)2,0(kxyPBPyP式为的解析故可设直线轴的正半轴上在又220,)1(OBPBPBCPB有如图示时当24)52(22221:21)0,4(xyPBkB的解析式为直线代入得又.)0,0(,,2)4,2(),0...