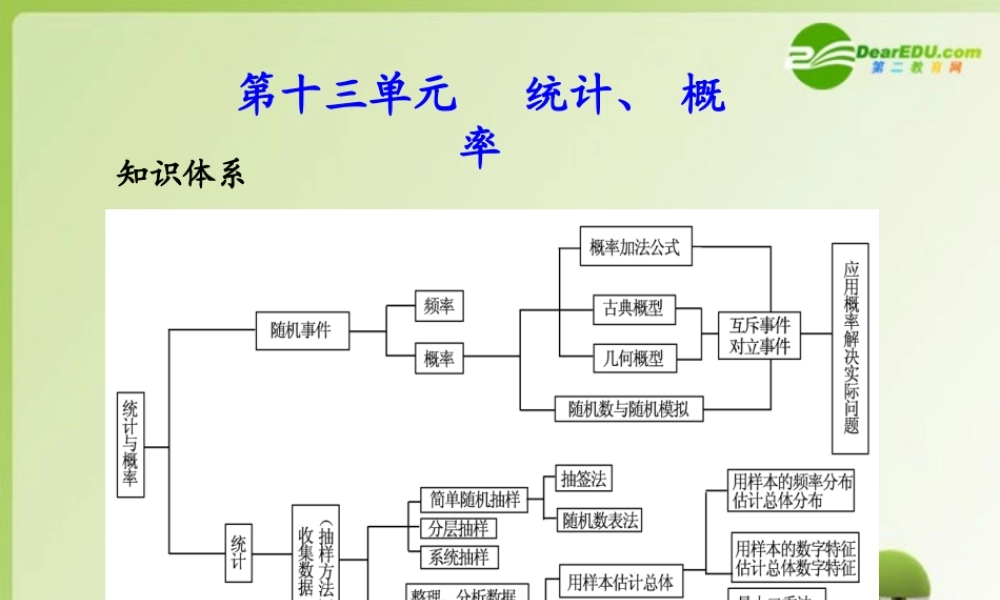
第十三单元 统计、 概率知识体系 第六节 几何概型基础梳理1. 几何概型的概念对于一个随机试验,我们将每个基本事件理解为从某个特定的几何区域内随机地取一点,该区域中每一点被取到的机会都一样 ; 而一个随机事件的发生则理解为恰好取到上述区域内的某个指定区域中的点,这里的区域可以是 、 、 等 . 用这种方法处理随机试验,称为几何概型 .2. 几何概型的特点( 1 )无限性:即在一次试验中,基本事件的个数可以是 .( 2 )等可能性:即每个基本事件发生的可能性是 .线段平面图形立体图形无限的均等的 因此,用几何概型求解的概率问题和古典概型的思路是相同的,同属于“比例解法” . 即随机事件 A 的概率可以用“事件 A 包含的基本事件所占的图形面积(体积、长度)”与“试验的基本事件所占的总面积(体积、长度)”之比来表示 .3. 几何概型的计算公式一般地,在几何区域 D 中随机取一点,记事件“该点落在其内部一个区域 d 内”为事件 A ,则事件 A 发生的概率 P(A)= .4. 几何概型与古典概型的区别与联系( 1 )共同点: .( 2 )不同点:基本事件的个数一个是无限的,一个是有限的 .基本事件可以抽象为点,对于几何概型,这些点尽管是无限的,但它们所占据的区域却是有限的,根据等可能性,这个点落在区域的概率与该区域的度量成正比,而与该区域的位置和形状无关 .D的测度d的测度基本事件都是等可能的 典例分析题型一 与长度有关的几何概型【例 1 】( 2009· 盐城模拟)某公共汽车站每隔 10 分钟有一辆汽车到达,乘客到达车站的时刻是任意的,求一个乘客候车时间不超过 7 分钟的概率 .分析 因为乘客在两车间隔的 10 分钟内任何时刻都可能到,所以该事件包含的基本事件是无限多个,并且每个事件发生的可能性都是一样的,故是几何概型问题 .解 每个乘客可在相邻两班车之间的任何一个时刻到达车站,因此每个乘客到达车站的时刻 t 可以看成是均匀落在长为 10 分钟的时间区间 (0,10] 上的一个随机点,等待时间不超过 7 分钟则是指点落在区间 [3,10] 上 . 如图所示 . 设第一辆车于时刻 T1 到达,而第二辆车于时刻 T2到达,线段 T1T2 的长度为 10 ,设 T 是线段 T1T2 上的点,且 TT2的长度等于 7. 记“等车时间不超过 7 分钟”为事件 A ,事件 A发生即点 t 落在线段 TT2 上,则 D 的长度 =T1T2=10,A 的长度 =TT2=7,所以 P ( A )...