0513高一数学(142-1函数的周期性) 高一数学全套课件 必修四VIP免费

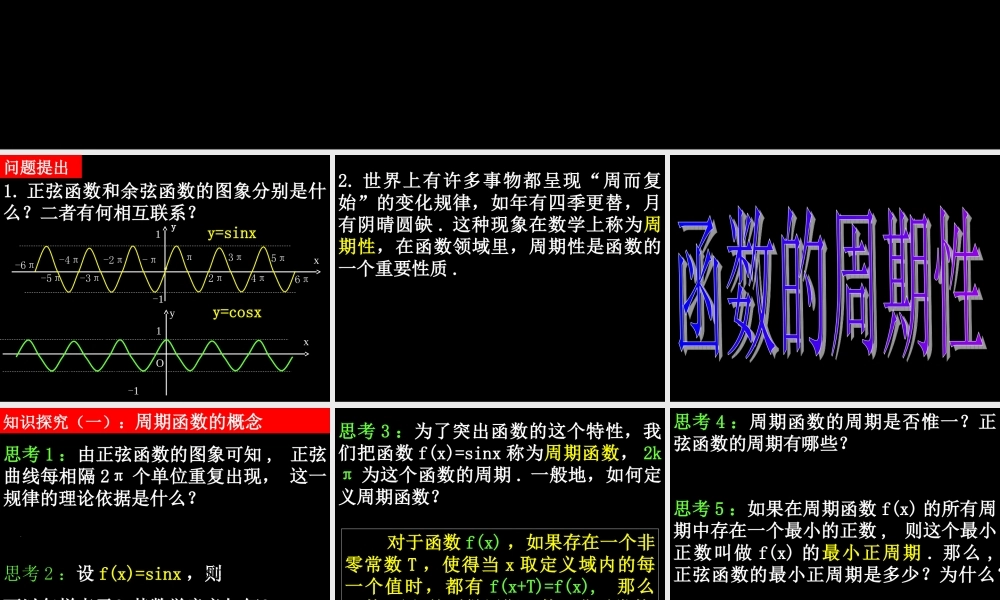
第一课时 1.4.2 正弦函数、余弦函数的性质 问题提出t57301p21. 正弦函数和余弦函数的图象分别是什么？二者有何相互联系？y-1xO1π2π3π4π5π6π-2π-3π-4π-5π-6π-πy=sinxxyO1-1222222222222y=cosx t57301p22. 世界上有许多事物都呈现“周而复始”的变化规律，如年有四季更替，月有阴晴圆缺 . 这种现象在数学上称为周期性，在函数领域里，周期性是函数的一个重要性质 . 知识探究（一）：周期函数的概念 思考 1 ：由正弦函数的图象可知 , 正弦曲线每相隔 2π 个单位重复出现， 这一规律的理论依据是什么？sin(2)sin()xkx kZ.思考 2 ：设 f(x)=sinx ，则 可以怎样表示？其数学意义如何？ sin(2)sinxkx 思考 3 ：为了突出函数的这个特性，我们把函数 f(x)=sinx 称为周期函数， 2kπ 为这个函数的周期 . 一般地，如何定义周期函数？ 对于函数 f(x) ，如果存在一个非零常数 T ，使得当 x 取定义域内的每一个值时，都有 f(x+T)=f(x), 那么函数 f(x) 就叫做周期函数，非零常数T 就叫做这个函数的周期 . 思考 4 ：周期函数的周期是否惟一？正弦函数的周期有哪些？思考 5 ：如果在周期函数 f(x) 的所有周期中存在一个最小的正数 , 则这个最小正数叫做 f(x) 的最小正周期 . 那么 , 正弦函数的最小正周期是多少？为什么？ 正、余弦函数是周期函数， 2kπ （ k∈Z, k≠0 ）都是它的周期，最小正周期是 2π ．思考 6 ：就周期性而言，对正弦函数有什么结论？对余弦函数呢？ 知识探究（二）：周期概念的拓展 思考 1 ：函数 f(x)=sinx （ x≥0 ）是否为周期函数？函数 f(x)=sinx （ x≤0 ）是否为周期函数？思考 2 ：函数 f(x)=sinx （ x>0 ）是否为周期函数？函数 f(x)=sinx （ x≠3kπ ）是否为周期函数？思考 3 ：函数 f(x)=sinx ， x∈[0 ， 10π] 是否为周期函数？周期函数的定义域有什么特点？ 思考 4 ：函数 y=3sin(2x ＋ 4) 的最小正周期是多少？ sin()yAxwj=+(0,0)Aw¹>思考 5 ：一般地，函数 的最小正周期是多少 ? 思考 6 ：如果函数 y=f(x) 的周期是 T ，那么函数 y=f(ωx ＋ φ) 的周期是多少？ 理论迁移 例 1 求下列函数的周期：（ 1 ） y=3cosx; x∈R（ 2 ） y=sin2x ， x∈R； 2sin(...