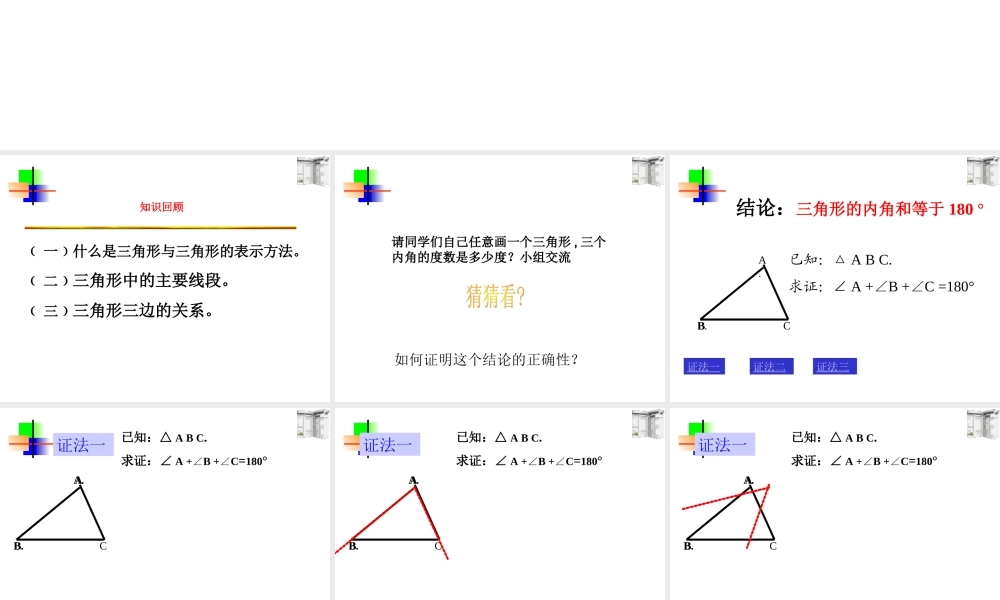
﹙ 一﹚什么是三角形与三角形的表示方法。﹙ 二﹚三角形中的主要线段。﹙ 三﹚三角形三边的关系。知识回顾 请同学们自己任意画一个三角形 , 三个内角的度数是多少度?小组交流如何证明这个结论的正确性? 结论:三角形的内角和等于 180 °已知:△ A B C.求证:∠ A +B +C =180°∠∠证法一证法三证法二A. BCB. ABC证法一已知:△ A B C.求证:∠ A +B +C∠∠ =180°A.B. ABC证法一A.B.已知:△ A B C.求证:∠ A +B +C∠∠ =180° ABC证法一已知:△ A B C.求证:∠ A +B +C∠∠ =180°A.B. ABC证法一已知:△ A B C.求证:∠ A +B +C∠∠ =180°A.B. ABC证法一已知:△ A B C.求证:∠ A +B +C∠∠ =180°A.B. ABC证法一已知:△ A B C.求证:∠ A +B +C∠∠ =180°A.B. ABC证法一已知:△ A B C.求证:∠ A +B +C∠∠ =180°A.B. ABC证法一已知:△ A B C.求证:∠ A +B +C∠∠ =180°A.B. E.D.证法一返回ABC证法一 则 C EB A ∥﹙ 内错角相等,两直线平行﹚ ∴ ∠D C E =B ∠﹙ 两直线平行,同位角相等﹚ ∠B C A +A C E +E C D =180°∠∠﹙ 平角定义﹚ ∴ ∠B C A +A +B = 180° ∠∠﹙ 等量代换﹚已知:△ A B C.求证:∠ A +B +C∠∠ =180°证明:在△ A B C 的外部以 C A 为边作∠ A C E. =A. ∠延长 B C 至 D 。A.B. E.D.证法一返回ABC证法一已知:△ A B C.求证:∠ A +B +C∠∠ =180°证明:在△ A B C 的外部以 C A 为边作∠ A C E. =A. ∠延长 B C 至 D 。 则 C EB A ∥﹙ 内错角相等,两直线平行﹚ ∴ ∠D C E =B ∠﹙ 两直线平行,同位角相等﹚ ∠B C A +A C E +E C D =180°∠∠﹙ 平角定义﹚ ∴ ∠B C A +A +B = 180° ∠∠﹙ 等量代换﹚A.B. BC证法二返回已知:△ A B C.求证:∠ A +B +C ∠∠=180°D E. 证明:延长 B C 至 D ,过 C 作 C EB A. ∥ 则∠ A =A C E ∠﹙ 两直线平行,内错角相等﹚ ∠ B =E C D ∠﹙ 两直线平行,同位角相等﹚ ∠ B C A +A C E +E C D =180° ∠∠﹙ 平角定义﹚ ∴ ∠B C A +A +B = 180° ∠∠﹙ 等量代换﹚ A.B. BC证法二返回已知:△ A B C.求证:∠ A +B +C ∠∠=180°D E. 证明:延长 B C...