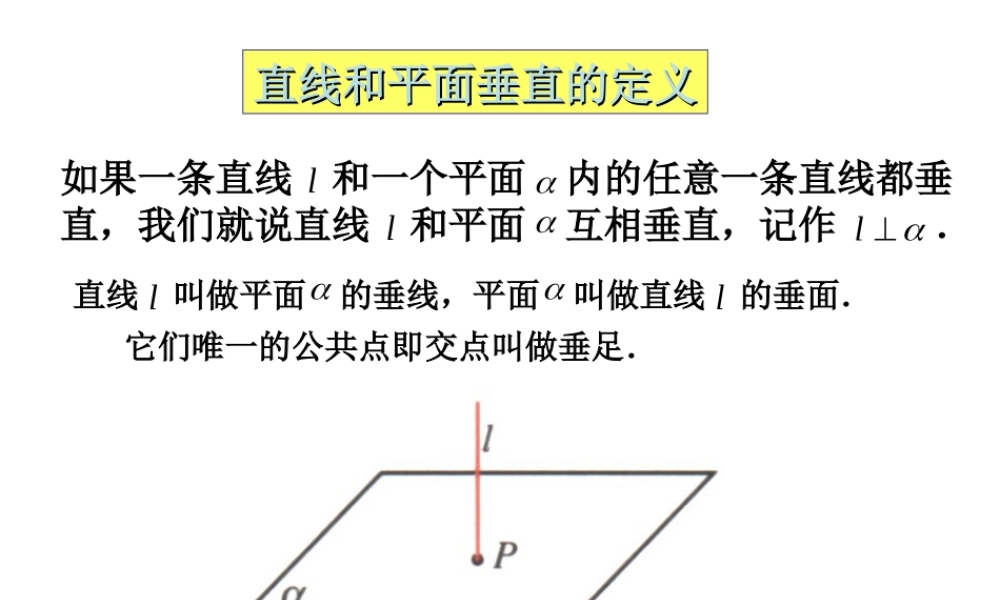
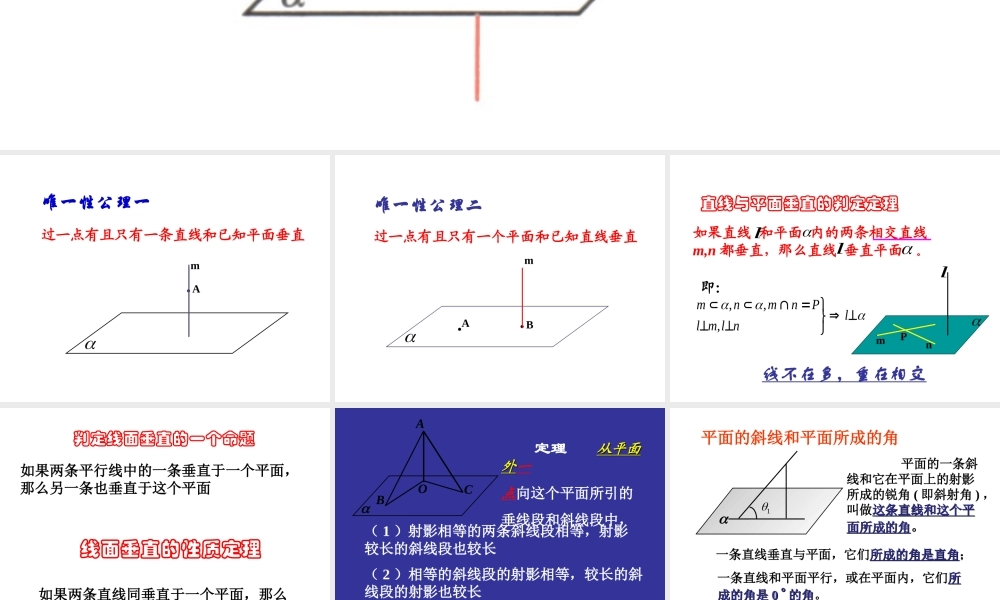
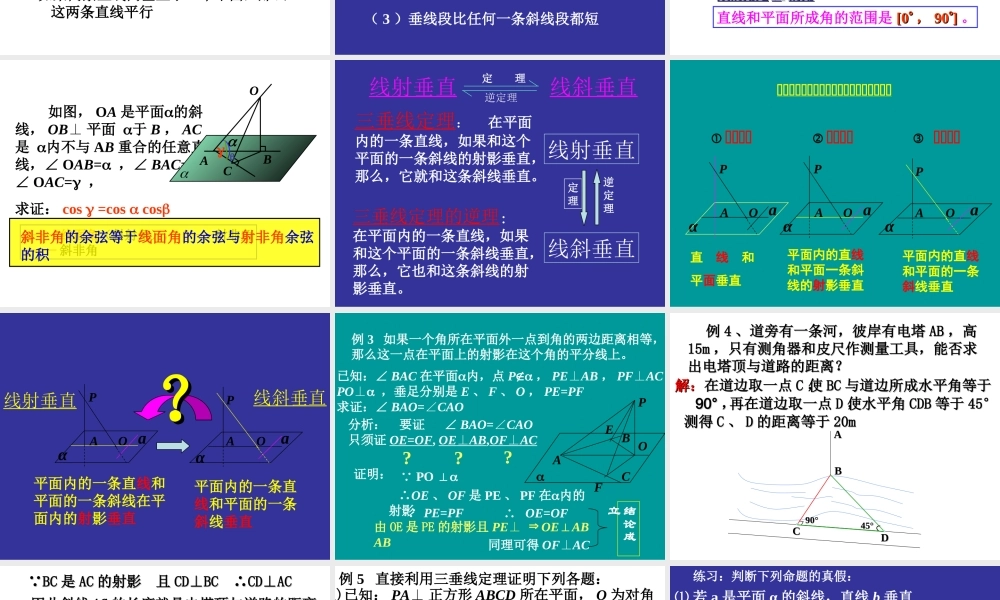
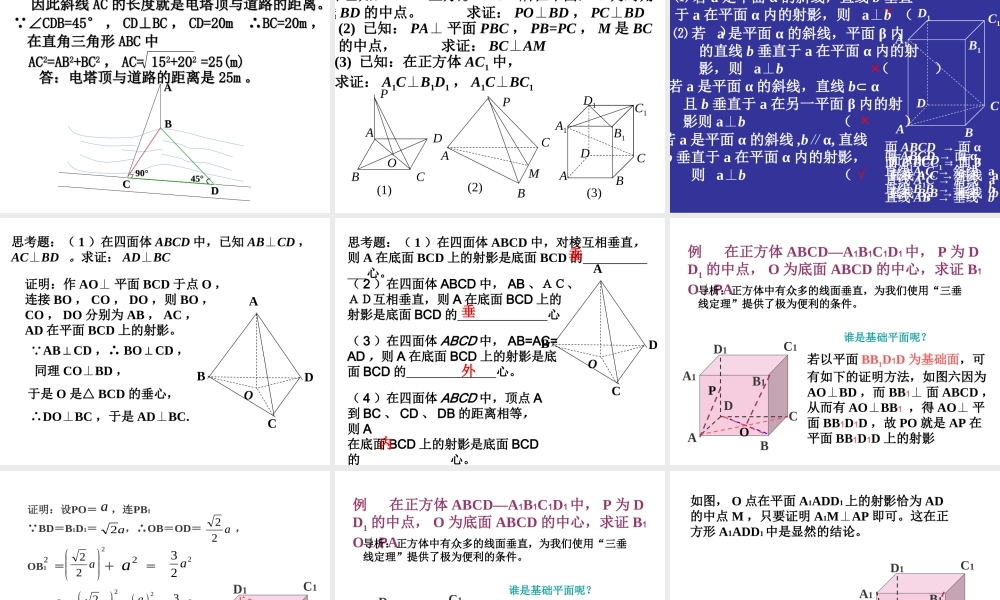
直线和平面垂直的定义直线和平面垂直的定义如果一条直线 和一个平面 内的任意一条直线都垂直,我们就说直线 和平面 互相垂直,记作 .lll它们唯一的公共点即交点叫做垂足.直线 叫做平面 的垂线,平面 叫做直线 的垂面. ll 唯一性公理一mA过一点有且只有一条直线和已知平面垂直 唯一性公理二过一点有且只有一个平面和已知直线垂直mAB 直线与平面垂直的判定定理lnlmlPnmnm,,,如果直线 和平面 内的两条相交直线m,n 都垂直,那么直线 垂直平面 。ll即:mnPl线不在多,重在相交 线面垂直的性质定理如果两条直线同垂直于一个平面,那么这两条直线平行判定线面垂直的一个命题如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于这个平面 ACBO 定理 从平面从平面外外一点向这个平面所引的垂线段和斜线段中,( 1 )射影相等的两条斜线段相等,射影较长的斜线段也较长( 2 )相等的斜线段的射影相等,较长的斜线段的射影也较长( 3 )垂线段比任何一条斜线段都短 平面的一条斜线和它在平面上的射影所成的锐角 ( 即斜射角 ) ,叫做这条直线和这个平这条直线和这个平面所成的角面所成的角。1一条直线垂直与平面,它们所成的角是直角所成的角是直角;一条直线和平面平行,或在平面内,它们所所成的角是成的角是 0 0 的角的角。直线和平面所成角的范围是 [0[0 ,, 9090]] 。平面的斜线和平面所成的角 如图, OA 是平面的斜线, OB⊥ 平面 于 B , AC是 内不与 AB 重合的任意直线,∠ OAB= ,∠ BAC= ,∠ OAC= ,求证: cos =cos cosOABC—— 线面角(斜射角), ——射非角—— 斜非角斜非角的余弦等于线面角的余弦与射非角余弦的积 三垂线定理的逆理: 在平面内的一条直线,如果和这个平面的一条斜线垂直,那么,它也和这条斜线的射影垂直。三垂线定理 :在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么,它就和这条斜线垂直。线射垂直线斜垂直定理逆定理线射垂直 线斜垂直 定 理逆定理 PAOaα三三三三三三三三三三三三三三三三三三三② 三三三三PAO aα① 三三三三③ 三三三三PAO aα直 线 和平面垂直平面内的直线和平面一条斜线的射影垂直平面内的直线和平面的一条斜线垂直 线射垂直线斜垂直PAOaαPAO aα平面内的一条直线和平...