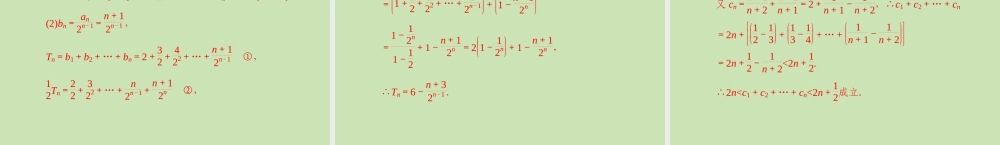(2) 等比数列 {an} 中, an = a1qn-1 ,第 7 讲 数列的综合应用用函数的观点理解等差、等比数列(1) 等差数列 {an} 中, an = a1 + (n - 1)d = dn + a1 - d ,当 d>0 时, {an} 是 _____ 数列, an 是 n 的一次函数;当 d = 0 时, {an} 是常数列, an 是 n 的常数函数;当 d<0 时, {an} 是 _____ 数列, an 是 n 的一次函数.当 a1>0 , q>1 或 a1<0,00,01 时, {an} 是 _____ 数列;当 q = 1 时, {an} 是一个常数列;当 q<0 时, {an} 是一个 ____数列.A . 12B . 13C . 14D . 15A .-12B .- 2C . 2D.12递减摆动 1 .若等差数列 {an} 的前 5 项和 S5 = 25 ,且 a2 = 3 ,则 a7 = ( )B2 .已知 {an} 是等比数列, a2 = 2 , a5 = ,则公比 q= ( )14D的前 10 项和为 ( )A . 2 -124B . 2 -129C . 2 -1210D . 2 - 12114 .已知等比数列 {an} 满足 a1 + a2 = 3 , a2 + a3 = 6 ,则 a7 = ( )A . 64B . 81C . 128D . 2435 .数列 {an} 是首项 a1 = 1 ,公差为 d = 3 的等差数列,如果an = 2 005 ,则序号 n 等于 ( )A . 667B . 668C . 669D . 6703 .在等比数列 {an}(n∈N*) 中,若 a1 = 1 , a4 = ,则该数列 18BA C考点 1 等差、等比数列的基本量运算例 1:等差数列{an}中,a4=10 且 a3、a6、a10 成等比数列,求数列{an}前 20 项的和 S20. 解析:设数列{an}的公差为 d,则 a3=a4-d=10-d, a6=a4+2d=10+2d,a10=a4+6d=10+6d. 由 a3、a6、a10 成等比数列得 a3a10=a26, 即(10-d)(10+6d)=(10+2d)2, 整理得 10d2-10d=0,解得 d=0 或 d=1. 综合运用等差、等比数列的有关公式和性质是解决等差、等比数列综合问题的关键.当 d=0 时,S20=20a4=200. 当 d=1 时,a1=a4-3d=10-3×1=7, 于是 S20=20a1+20×192d=20×7+190=330. 【互动探究】1.等差数列{an}的前 n 项和记为 Sn.已知 a10=30,a20=50. (1)求通项 an; (2)若 Sn=242,求 n. 解:(1)由 an=a1+(n-1)d,a10=30,a20=50,得方程组 a1+9d=3...