(高考风向标)高考数学一轮复习 第六章 第2讲 同角三角函数的基本关系式与诱导公式精品课件 文 课件VIP免费

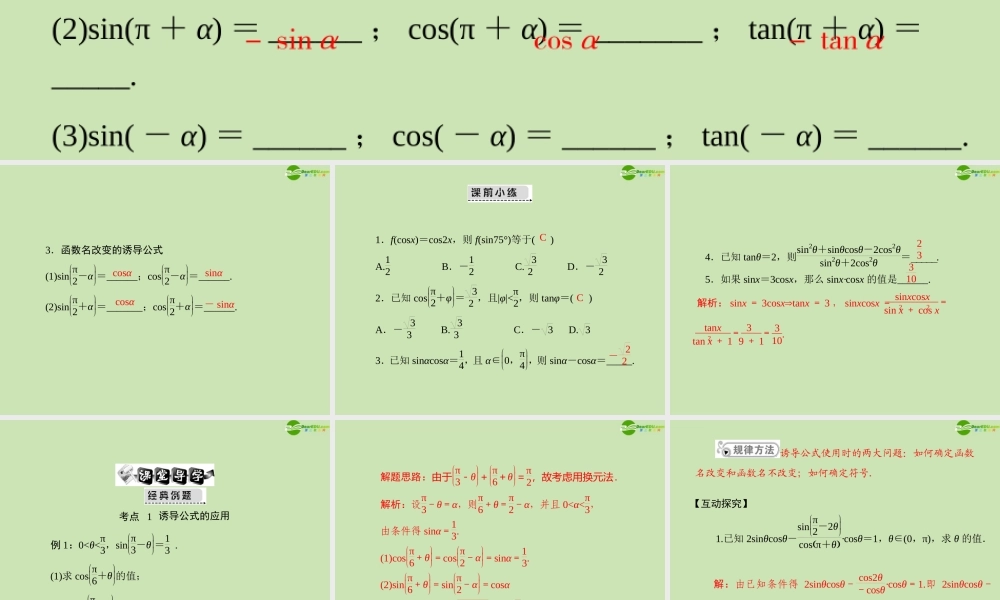
平方关系： _______________;第 2 讲 同角三角函数的基本关系式与诱导公式1 ．同角三角函数关系式商数关系： ____________.＝ tanαsinαcosα2 ．函数名不变的诱导公式(1)sin(π － α) ＝ _____ ； cos(π － α) ＝ ______ ； tan(π － α) ＝_______.(2)sin(π ＋ α) ＝ ______ ； cos(π ＋ α) ＝ _______ ； tan(π ＋ α) ＝_____.(3)sin( － α) ＝ ______ ； cos( － α) ＝ ______ ； tan( － α) ＝ ______.sin 2α ＋ cos2 α ＝1sinα－ cosα－ tanα－ sinα－ cosαtanα－ sinαcosα－ tanα3．函数名改变的诱导公式 (1)sinπ2－α ＝______；cosπ2－α ＝______. (2)sinπ2＋α ＝_______；cosπ2＋α ＝______. － sinαcosαsinαcosαCC1．f(cosx)＝cos2x，则 f(sin75°)等于( ) A.12 B．－12 C. 32 D．－ 32 2．已知 cosπ2＋φ ＝ 32 ，且|φ|<π2，则 tanφ＝( ) A．－ 33 B. 33 C．－ 3 D. 3 3．已知 sinαcosα＝14，且 α∈0，π4 ，则 sinα－cosα＝_____. － 22 ＝sin x ＋ cos x＝tan x ＋ 1＝解析： sinx ＝ 3cosx t⇒ anx ＝ 3 ， sinxcosx ＝ sinxcosx2 2tanx239 ＋ 13 .1023 310 4．已知 tanθ＝2，则sin2θ＋sinθcosθ－2cos2θsin2θ＋2cos2θ＝_____. 5．如果 sinx＝3cosx，那么 sinx·cosx 的值是______. 考点 1 诱导公式的应用例 1：0<θ<π3，sinπ3－θ ＝13 . (1)求 cosπ6＋θ 的值； (2)求 sinπ6＋θ 的值． 解题思路：由于π3－θ ＋π6＋θ ＝π2，故考虑用换元法． 解析：设π3－θ＝α，则π6＋θ＝π2－α，并且 0<α<π3， 由条件得 sinα＝13. (1)cosπ6＋θ ＝cosπ2－α ＝sinα＝13. (2)sinπ6＋θ ＝sinπ2－α ＝cosα ＝ 1－sin2α＝1－132＝2 23. 诱导公式使用时的两大问题：如何确定函数名改变和函数名不改变；如何确定符号．【互动探究】解：由已知条件得 2sinθcosθ－ cos2θ－cosθ·cosθ＝1.即 2sinθcosθ－2sin2θ＝0.解得 tanθ＝1.由 0＜θ＜π 知，从而 θ＝π4. 1.已知 2si...