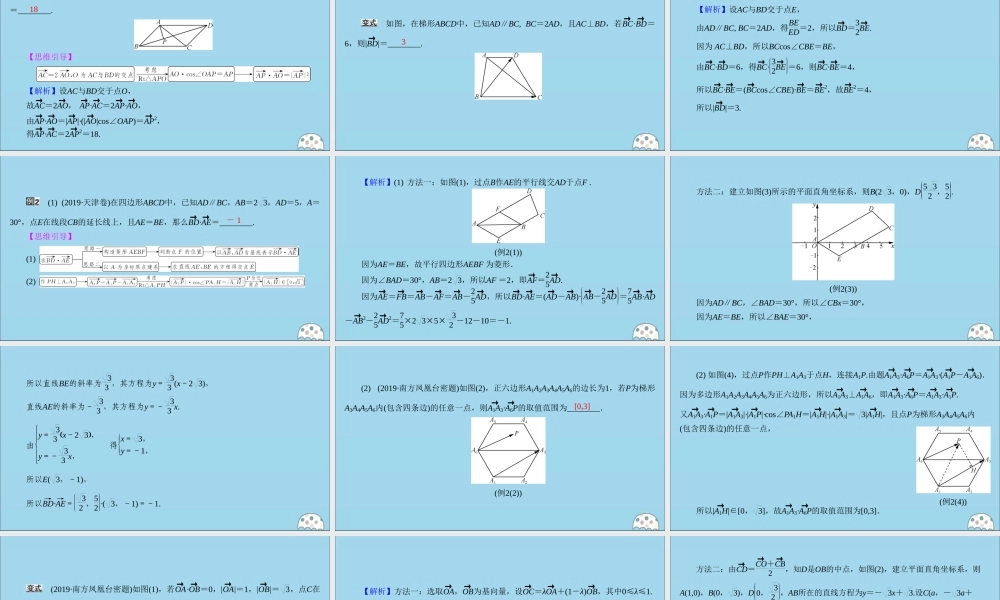
专题一 三角函数和平面向量 微切口 6 几何图形中数量积的应用 如图,在平行四边形ABCD中,若AP⊥BD,垂足为P,且AP=3,则 AP→ ·AC→=________. 【思维引导】 18 【解析】设AC与BD交于点O, 故AC→2= AO→ , AP→·AC→2= AP→·AO→ , 由AP→·AO→|= AP→|·(|AO→ |cos∠OAP)=AP→ 2, 得AP→·AC→2= AP→ 218.= 如图,在梯形ABCD中,已知AD∥BC, BC=2AD,且AC⊥BD,若BC→ ·BD→ =6,则|BD→ |=________. 3 【解析】设AC与BD交于点E, 由AD∥BC, BC2= AD,得BEED2= ,所以BD→ =32BE→. 因为 AC⊥BD,所以BCcos∠CBE=BE, 由BC→·BD→6= ,得BC→·32BE→6= ,则BC→·BE→4= , 所以BC→·BE→(= BC→cos∠CBE)·BE→=BE→ 2,故BE→ 24= , |所以 BD→ |=3. (1) (2019·天津卷)在四边形ABCD中,已知AD∥BC,AB=2 3,AD=5,A=30°,点E在线段CB的延长线上,且AE=BE,那么BD→ ·AE→=________. 【思维引导】 (1) (2) - 1 【解析】(1) 方法一:(1)如图,过点B作AE的平行线交AD于点F . (例2(1)) 因为AE=BE,故平行四边形AEBF 为菱形. 因为∠BAD30°=,AB2=3,所以AF 2= ,即AF→=25AD→ . 因为AE→=FB→=AB→-AF→=AB→-25AD→ ,所以BD→ ·AE→(= AD→ -AB→)·AB→-25AD→ =75AB→·AD→-AB→ 2-25AD→ 2=75×2 3×5× 3212101.--=- 方法二:(3)建立如图所示的平面直角坐标系,则B(2 30),,D5 32 ,52 . (2(3))例 因为AD∥BC,∠BAD30°=,所以∠CBx30°=, 因为AE=BE,所以∠BAE30°=, 所以直线BE的斜率为 33 ,其方程为y= 33 (x-2 3), 直线AE的斜率为- 33 ,其方程为y=- 33 x. 由 y= 33 x-2 3,y=- 33 x,得 x= 3,y=-1, 所以E( 3,-1), 所以BD→ ·AE→=32 ,52 ·( 3,-1)=-1. (2) (2019·南方凤凰台密题)如图(2),正六边形A1A2A3A4A5A6的边长为1,若P为梯形A3A4A5A6内(包含四条边)的任意一点,则A1A3→ ·A6P→ 的取值范围为________. (例2(2)) [0,3] (2) (4)如图,过点P作PH⊥A1A3于点H,连接A1P.由题A1A3→ ·A6P→ =A1A3→ ·(A1P→ -A1A6→ ). 因为多边形A1A2A3A4A5A6为正六边形,所以A1A3→ ⊥A1A6→ ,即A1A3→ ...