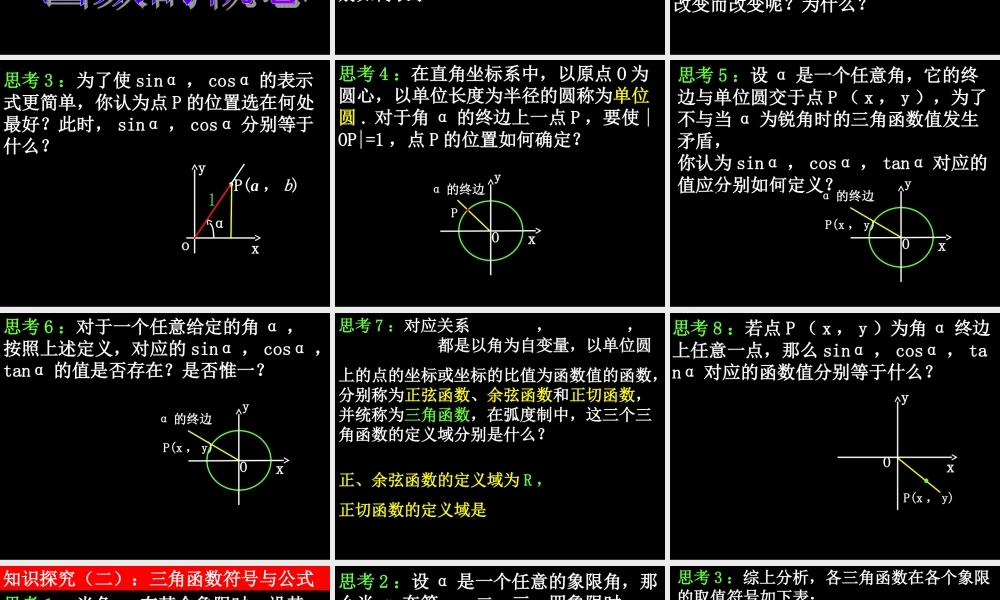
1.2 任意角的三角函数 1.2.1 任意角的三角函数第一课时 问题提出1. 角的概念是由几个要素构成的,具体怎样理解? ( 1 )角是由平面内一条射线绕其端点从一个位置旋转到另一个位置所组成的图形 .( 2 )按逆时针方向旋转形成的角为正角,按顺时针方向旋转形成的角为负角,没有作任何旋转形成的角为零角 .( 3 )角的大小是任意的 . 2. 什么叫做 1 弧度的角?度与弧度是怎样换算的?( 1 )等于半径长的圆弧所对的圆心角叫做1 弧度的角 . 3. 与角 α 终边相同的角的一般表达式是什么?2()kkZbap=+Îβ=α + k·360° ( k∈Z )或 2()kkZbap=+Î( 2 ) 180° = rad. 4. 如图,在直角三角形 ABC 中, sinα ,cosα , tanα 分别叫做角 α 的正弦、余弦和正切,它们的值分别等于什么?ABCα5. 当角 α 不是锐角时,我们必须对 sinα , cosα , tanα 的值进行推广,以适应任意角的需要 . sinBCABa =cosACABa =tanBCACa = 知识探究(一):任意角的三角函数 思考 1 :为了研究方便,我们把锐角α 放到直角坐标系中,并使角 α 的顶点与原点 O 重合 , 始边与 x 轴的非负半轴重合 . 在角 α 的终边上取一点 P( a , b ) , 设点 P 与原点的距离为 r ,那么, sinα , cosα , tanα 的值分别如何表示? sinbr sinbr sinbr cosar cosar tanba tanba 思考 2 :对于确定的角 α ,上述三个比值是否随点 P 在角 α 的终边上的位置的改变而改变呢?为什么? xyoP(a , b)αrAB 思考 3 :为了使 sinα , cosα 的表示式更简单,你认为点 P 的位置选在何处最好?此时, sinα , cosα 分别等于什么?xyoP(a , b)αsinb cosa tanba 1 思考 4 :在直角坐标系中,以原点 O 为圆心,以单位长度为半径的圆称为单位圆 . 对于角 α 的终边上一点 P ,要使 |OP|=1 ,点 P 的位置如何确定? α 的终边OxyP 思考 5 :设 α 是一个任意角,它的终边与单位圆交于点 P ( x , y ),为了不与当 α 为锐角时的三角函数值发生矛盾,你认为 sinα , cosα , tanα 对应的值应分别如何定义? α 的终边P(x , y)Oxysiny cosx tan(0)y xx 思考 6 :对于一个任意给定的角 α ,按照上述定义,对应的 sinα...