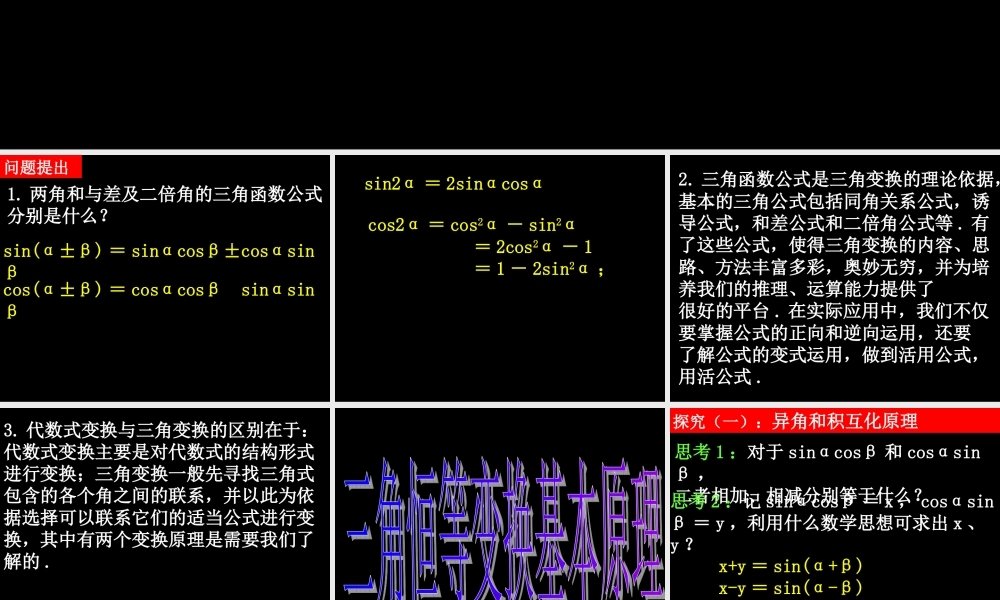
3.2 简单的三角恒等变换第一课时 问题提出t57301p21. 两角和与差及二倍角的三角函数公式分别是什么?sin(α±β) = sinαcosβ±cosαsinβ tantan1tantan)(tancos(α±β) = cosαcosβ sinαsinβ m cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α ; 2tan1tan22tan2tan1tan22tan2tan1tan22tan2tan1tan22tan2tan1tan22tan2tan1tan22tansin2α = 2sinαcosα 2. 三角函数公式是三角变换的理论依据,基本的三角公式包括同角关系公式,诱导公式,和差公式和二倍角公式等 . 有了这些公式,使得三角变换的内容、思路、方法丰富多彩,奥妙无穷,并为培养我们的推理、运算能力提供了很好的平台 . 在实际应用中,我们不仅要掌握公式的正向和逆向运用,还要了解公式的变式运用,做到活用公式,用活公式 . 3. 代数式变换与三角变换的区别在于:代数式变换主要是对代数式的结构形式进行变换;三角变换一般先寻找三角式包含的各个角之间的联系,并以此为依据选择可以联系它们的适当公式进行变换,其中有两个变换原理是需要我们了解的 . 探究(一):异角和积互化原理 思考 1 :对于 sinαcosβ 和 cosαsinβ ,二者相加、相减分别等于什么?思考 2 :记 sinαcosβ = x , cosαsinβ = y ,利用什么数学思想可求出 x 、y ?x+y = sin(α+β) x-y = sin(α-β){方程思想 左边是积右边是和差,从左到右积化和差 .思考 3 :由上述分析可知[]1cossinsin()sin()2ababab=+--)sin()sin(21cossin这两个等式左右两边的结构有什么特点?从左到右的变换功能是什么? 思考 4 令 , ,并交换等式两边的式子可得什么结论?sinsin2sincos22qjqjqj+-+=sinsin2cossin22qjqjqj+--=思考 5 :这两个等式左右两边的结构有什么特点?从左到右的变换功能是什么? 思考 6 :参照上述分析, cosαcosβ ,sinαsinβ 分别等于什么?其变换功能如何?[]1coscoscos()cos()2ababab=++-[]1sinsincos()cos()2ababab= -+-- 思考 7 : cosθ + cosφ , cosθ - cosφ分别等于什么?其变换功能如何?coscos2coscos22qjqjqj+-+=coscos2sinsin22qjqjqj+--= - 思考 8 :上述关系表明,两个不同的三角函数的和(差)与积...