七年级数学上册 4.5 最基本的图形—点和线 4.5.2 线段的长短比较教学课件 (新版)华东师大版 课件VIP免费

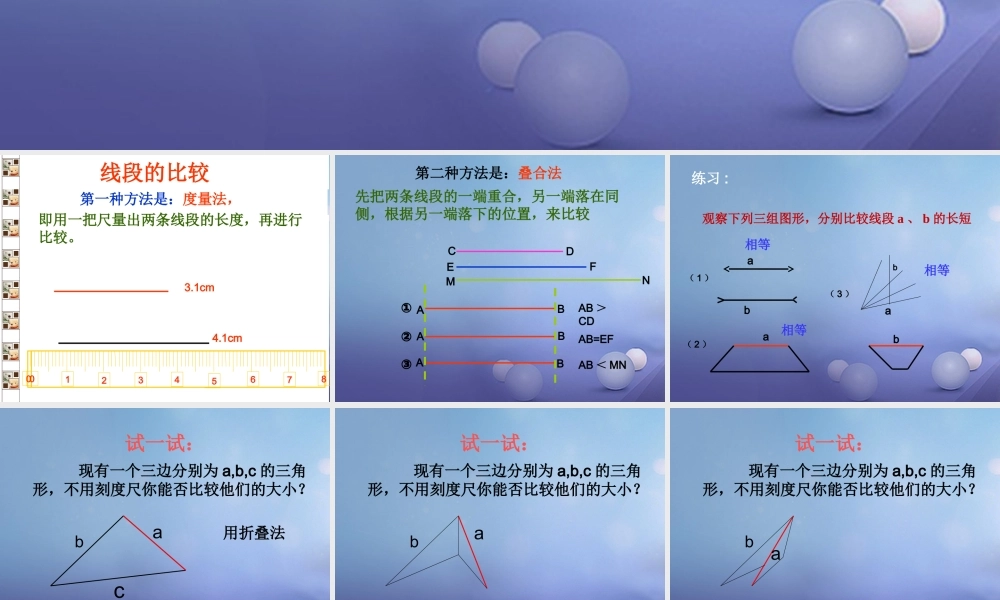
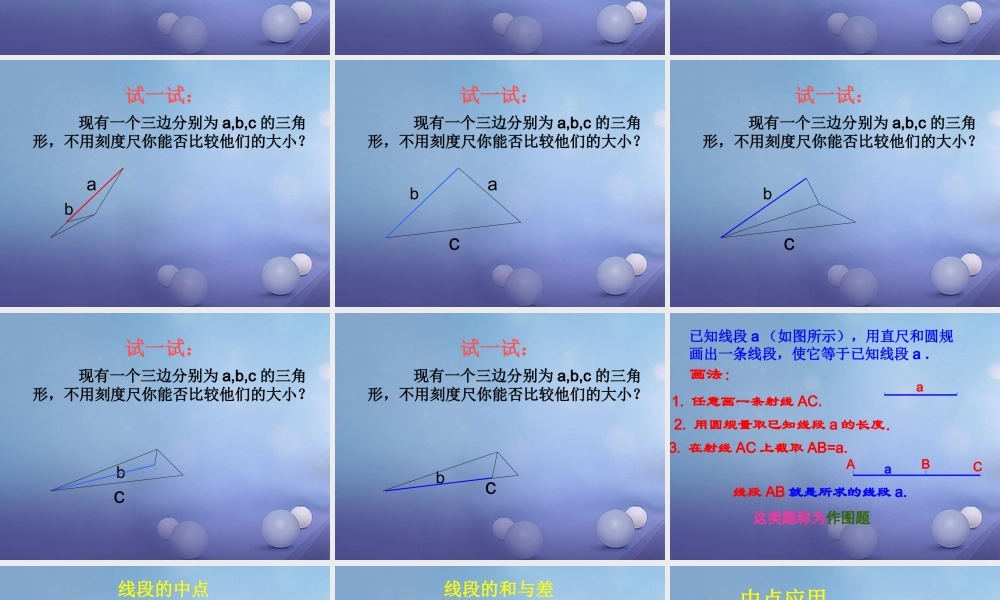
第一种方法是：度量法，1235467803.1cm4.1cm123546780线段的比较即用一把尺量出两条线段的长度，再进行比较。第二种方法是：叠合法①②③ABBAABCDEFMNAB ＞CDAB=EFAB ＜ MN先把两条线段的一端重合，另一端落在同侧，根据另一端落下的位置，来比较练习 : 观察下列三组图形，分别比较线段 a 、 b 的长短（ 1 ）ab（ 3 ）（ 2 ）abab相等相等相等试一试： 现有一个三边分别为 a,b,c 的三角形，不用刻度尺你能否比较他们的大小？abc用折叠法试一试： 现有一个三边分别为 a,b,c 的三角形，不用刻度尺你能否比较他们的大小？ab试一试： 现有一个三边分别为 a,b,c 的三角形，不用刻度尺你能否比较他们的大小？ab试一试： 现有一个三边分别为 a,b,c 的三角形，不用刻度尺你能否比较他们的大小？ab试一试： 现有一个三边分别为 a,b,c 的三角形，不用刻度尺你能否比较他们的大小？abc试一试： 现有一个三边分别为 a,b,c 的三角形，不用刻度尺你能否比较他们的大小？bc试一试： 现有一个三边分别为 a,b,c 的三角形，不用刻度尺你能否比较他们的大小？bc试一试： 现有一个三边分别为 a,b,c 的三角形，不用刻度尺你能否比较他们的大小？bc已知线段 a （如图所示），用直尺和圆规画出一条线段，使它等于已知线段 a ．a画法：1. 任意画一条射线 AC.2. 用圆规量取已知线段 a 的长度．3. 在射线 AC 上截取 AB=a.ACB线段 AB 就是所求的线段 a.a这类题称为作图题把一条线段分成两条相等线段的点，叫做这条线段的中点。线段的中点ABC如图，若 C 为线段 AB 的中点，则有如下等式成立：（ 1 ） AC=CB（ 2 ） AC=CB= AB 21（ 3 ） AB=2AC=2CB含义：“和”指线段数量的“和”与图形的“和”。“差”也如此。线段的和与差ABC如图，（ 1 ） AB=AC+CB（ 2 ） AC=AB-CB CB=AB-AC注意：线段的“和”或者“差”仍然是一条线段 1. 在下图中，点 C 是线段 AB 的中点。如果 AB=4cm ，那么 AC= ， BC= 。∴AC=CB=2cm AC+CB=AB=4cm中点应用ABC 2. 如图， AB=6cm ，点 C 是线段 AB 的中点，点 D 是线段 CB 的中点，那么 AD 有多长呢？cmCBCD5.121∴AC=CB= cmAB321cmCDACAD5.4ADCB解： 点 C 是线段 AB 的中点中点应用 答： AD 的长度为 4.5cm 点 D 是线段 CB 的中点还有其他的解法吗？解法二： 点 C 是线段 AB 的中点cmCBBD5.121...