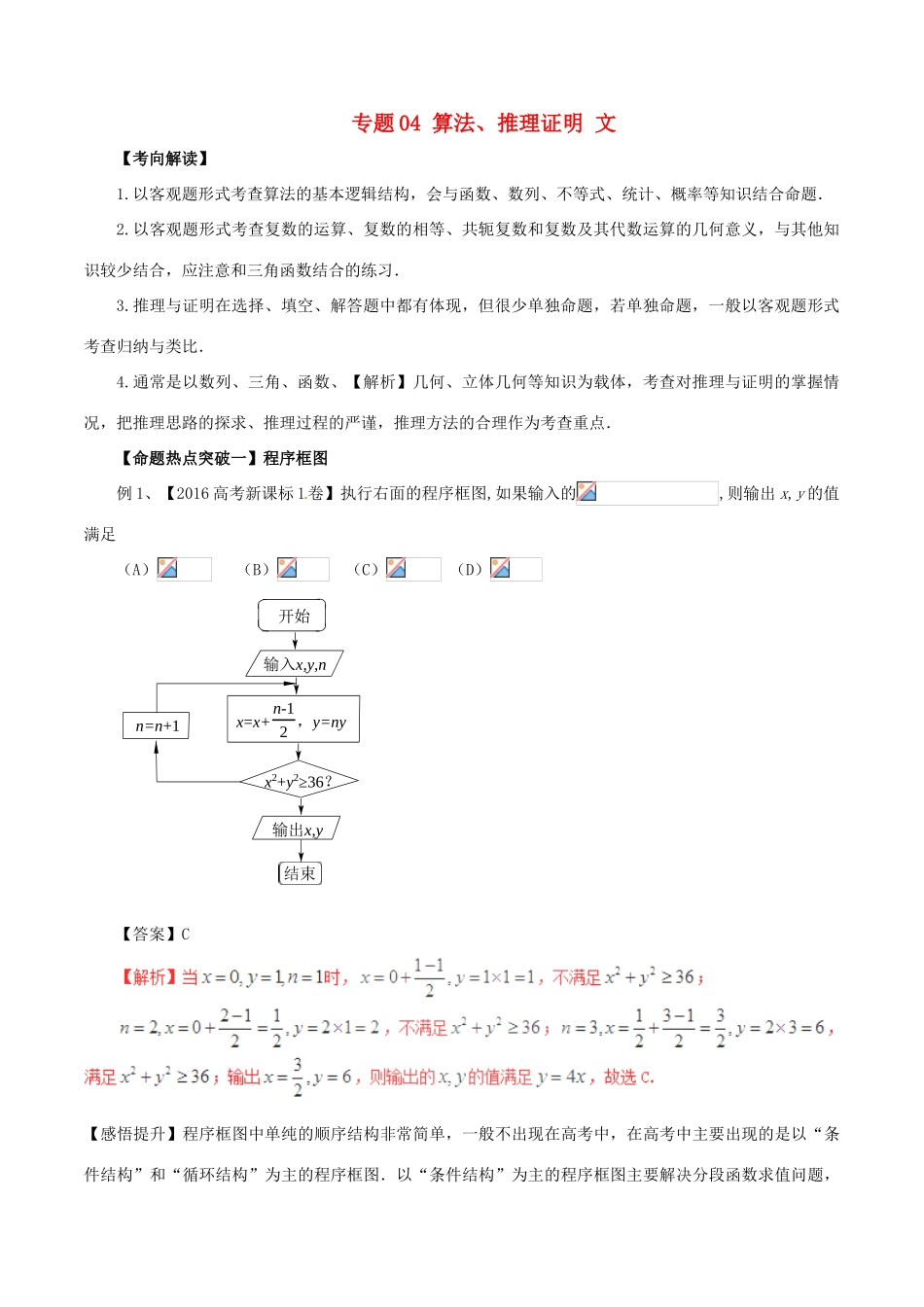
专题 04 算法、推理证明 文【考向解读】 1.以客观题形式考查算法的基本逻辑结构,会与函数、数列、不等式、统计、概率等知识结合命题.2.以客观题形式考查复数的运算、复数的相等、共轭复数和复数及其代数运算的几何意义,与其他知识较少结合,应注意和三角函数结合的练习.3.推理与证明在选择、填空、解答题中都有体现,但很少单独命题,若单独命题,一般以客观题形式考查归纳与类比.4.通常是以数列、三角、函数、【解析】几何、立体几何等知识为载体,考查对推理与证明的掌握情况,把推理思路的探求、推理过程的严谨,推理方法的合理作为考查重点.【命题热点突破一】程序框图例 1、【2016 高考新课标 1卷】执行右面的程序框图,如果输入的,则输出 x,y 的值满足(A) (B) (C) (D)n=n+1结束输出x,yx2+y2≥36?x=x+n-12 ,y=ny输入x,y,n开始【答案】C【感悟提升】程序框图中单纯的顺序结构非常简单,一般不出现在高考中,在高考中主要出现的是以“条件结构”和“循环结构”为主的程序框图.以“条件结构”为主的程序框图主要解决分段函数求值问题,以“循环结构”为主的程序框图主要解决数列求和、统计求和、数值求积等运算问题,这两种类型的程序框图中,关键因素之一就是“判断条件”,在解题中要切实注意判断条件的应用.【变式探究】 某程序框图如图 所示,若该程序运行后输出的 S 的值为 72,则判断框内填入的条件可以是( )A.n≤8? B.n≤9? C.n≤10? D.n≤11?【答案】A 【命题热点突破二】合情推理与演绎推理例 2、(1)观察下列各式:C=40;C+C=41;C+C+C=42;C+C+C+C=43;……照此规律,当 n∈N*时,C+C+C+…+C=________.(2)我们把平面内与直线垂直的非零向量称为直线的法向量,在平面直角坐标系中,利用求动点轨迹方程的方法可以求出过点 A(-2,3),且法向量为 n=(-1,2)的直线方程为(-1)×(x+2)+2×(y-3)=0,化简得 x-2y+8=0.类比上述方法,在空间直角坐标系中,经过点 A(1,2,3),且法向量为 n=(-1,2,-3)的平面的方程为________.【答案】(1)4n-1 (2)x-2y+3z-6=0 【解析】(1)归纳可知,C+C+C+…+C=4n-1.(2)类比直线方程的求解方法,可得平面的方程为(-1)×(x-1)+2×(y-2)+(-3)×(z-3)=0,即 x-2y+3z-6=0.【感悟提升】由特殊结论得出一般结论的推理是归纳推理,归纳出的一般性结论要包含已知的特殊结论;根据已有结...