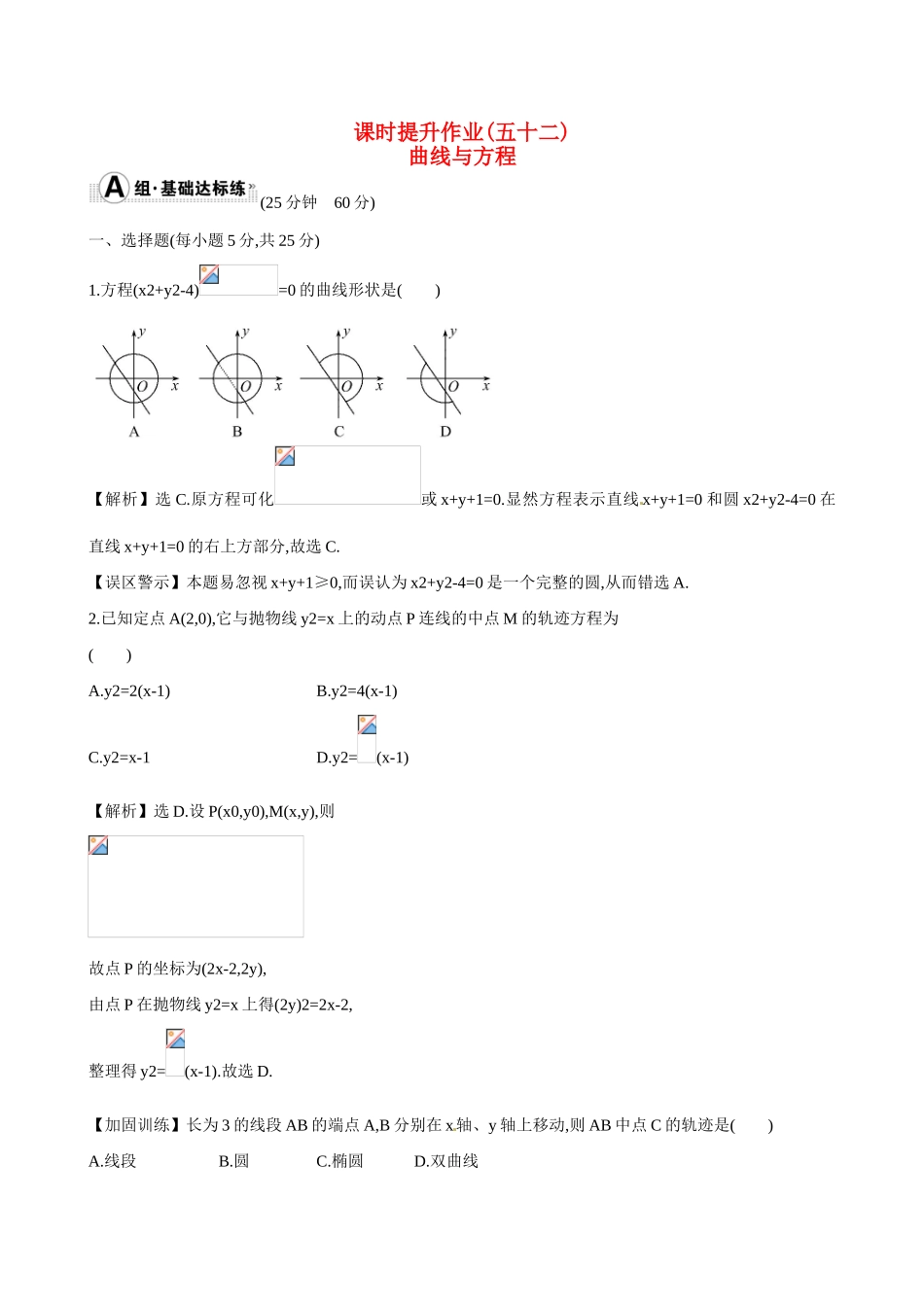
课时提升作业(五十二)曲线与方程(25 分钟 60 分)一、选择题(每小题 5 分,共 25 分)1.方程(x2+y2-4)=0 的曲线形状是( )【解析】选 C.原方程可化或 x+y+1=0.显然方程表示直线 x+y+1=0 和圆 x2+y2-4=0 在直线 x+y+1=0 的右上方部分,故选 C.【误区警示】本题易忽视 x+y+1≥0,而误认为 x2+y2-4=0 是一个完整的圆,从而错选 A.2.已知定点 A(2,0),它与抛物线 y2=x 上的动点 P 连线的中点 M 的轨迹方程为( )A.y2=2(x-1)B.y2=4(x-1)C.y2=x-1D.y2=(x-1)【解析】选 D.设 P(x0,y0),M(x,y),则故点 P 的坐标为(2x-2,2y),由点 P 在抛物线 y2=x 上得(2y)2=2x-2,整理得 y2=(x-1).故选 D.【加固训练】长为 3 的线段 AB 的端点 A,B 分别在 x轴、y 轴上移动,则 AB 中点 C 的轨迹是( )A.线段B.圆C.椭圆D.双曲线【解析】选 B.设 C(x,y),A(a,0),B(0,b),则 x=,y=,即 a=2x,b=2y.代入 a2+b2=9,得 4x2+4y2=9,即 x2+y2=.3.(2015·洛阳模拟)设过点 P(x,y)的直线分别与 x 轴的正半轴和 y 轴的正半轴交于 A,B 两点,点 Q 与点 P 关于y 轴对称,O 为坐标原点.若=2,且·=1,则点 P 的轨迹方程是( )A.x2+3y2=1(x>0,y>0)B.x2-3y2=1(x>0,y>0)C.3x2-y2=1(x>0,y>0)D.3x2+y2=1(x>0,y>0)【解题提示】利用点 Q 与点 P 关于 y 轴对称求得 Q 点的坐标,然后利用=2,·=1 即可求出点 P 的轨迹方程.【解析】选 A.设 A(a,0),B(0,b),a>0,b>0.由=2,得(x,y-b)=2(a-x,-y),即 a=x>0,b=3y>0.点 Q(-x,y),故由·=1,得(-x,y)·(-a,b)=1,即 ax+by=1.将 a,b 代入 ax+by=1 得所求的轨迹方程为x2+3y2=1(x>0,y>0).4.(2015·长春模拟)设圆(x+1)2+y2=25 的圆心为 C,A(1,0)是圆内一定点,Q 为圆周上任一点.线段 AQ 的垂直平分线与 CQ 的连线交于点 M,则点 M 的轨迹方程为( )A.=1B.=1C.=1D.=1【解析】选 D.因为 M 为 AQ 垂直平分线上一点,则|AM|=|MQ|,所以|MC|+|MA|=|MC|+|MQ|=|CQ|=5,故点 M 的轨迹为椭圆.所以 a=,c=1,则 b2=a2-c2=,所以椭圆的标准方程为=1.【加固训练】如图所示,A 是圆 O 内一定点,B 是圆周上一个动点,AB 的中垂线 CD 与 OB 交于点 E,则点 E的轨迹是( )A.圆B.椭圆C.双曲线D.抛物线【解析】选 B.由题意知,|EA|+|EO|=|EB|+|EO|=r(r 为圆的半径)且 r>|OA|,故 E 的轨迹为以 O,A 为焦点的椭圆,故选 B.5.已知定点 A(1,0)和定直线 l:x=-1,在 l 上有两动点 E,F ...