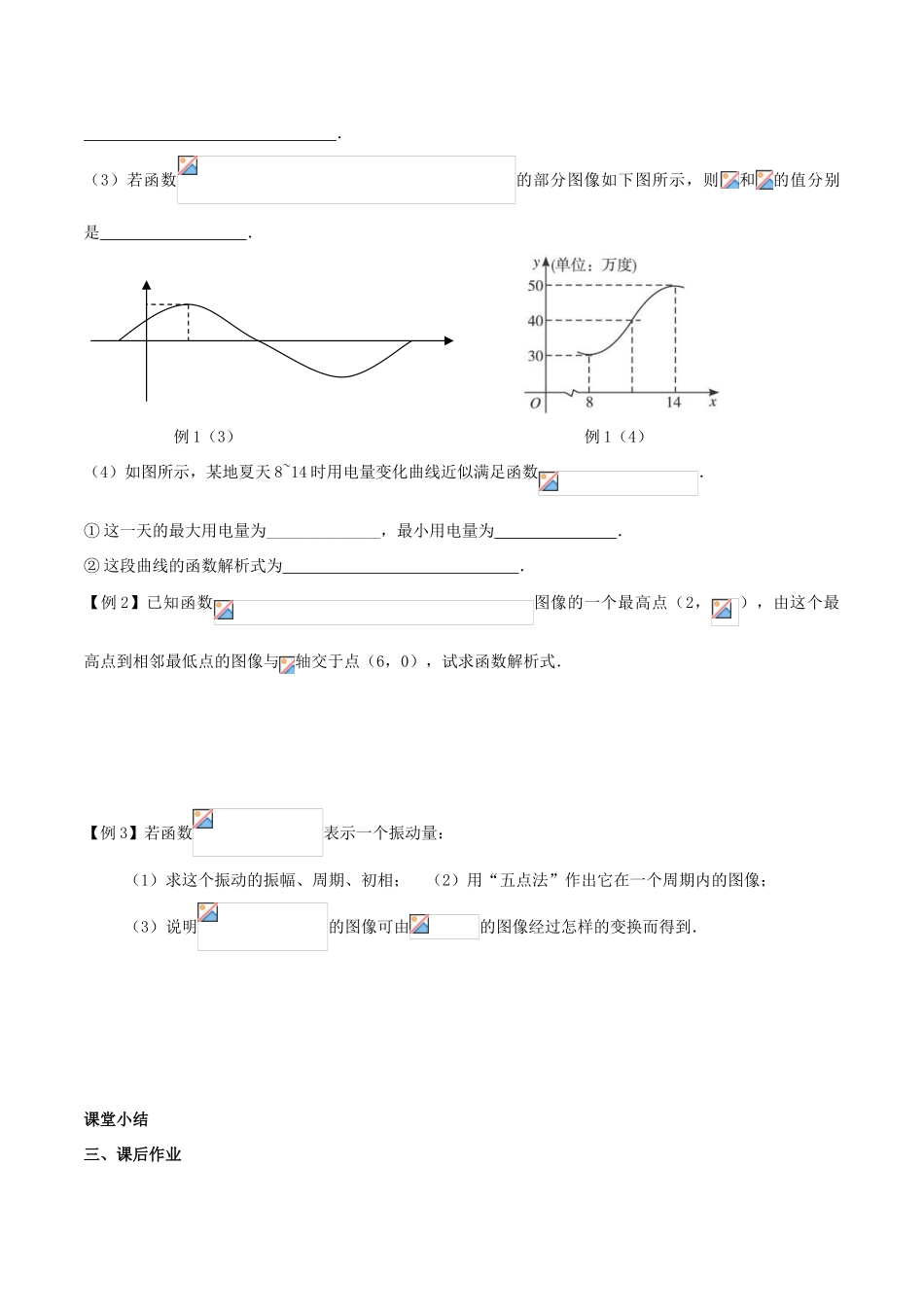
三角函数的图象(五点作图法与图象变换)一、课前准备:【自主梳理】1.简谐运动的有关概念简谐运动图像的解析式振幅周期频率相位初相2.“五点法”作图① 先确定周期 ,在一个周期内作出图像;②将分别取 , , , , 来求出对应的的值,列表;③描点画图,再利用函数的周期性,可把所得简图向左右分别扩展,从而得到的简图.3.三角函数图像变换(1)振幅变换;(2)周期变换;(3)相位变换;(4)平移变换.4.由得图像得到的图像的过程途径一:先平移变换再周期变换.途径二:先周期变换再平移变换 .【自我检测】1.若函数表示一个振动量,则其振幅为 ,周期为 ,初相为 .2.在确定函数在上的图像形状时,起关键作用的五个点是 、 、 、 、 . 3 . 为 了 得 到 函 数的 图 像 , 只 需 把 函 数的 图 像 上 所 有 的 点 . 4.把函数的图像上所有点的横坐标变为原来的倍,纵坐标不变,则所得的图像的函数解析式为 .5.将函数的图像上所有的点向右平行移动个单位长度,再把所得各点的横坐标伸长到原来的2 倍(纵坐标不变),所得图像的函数解析式是 .6 . 若 函 数的 部 分 图 像 如 下 图 所 示 , 则得解析式为 .二、课堂活动:【例 1】填空题:(1)把函数的图像向右平移个单位,所得到的图像的函数解析式为 ,再将图像上的所有点的横坐标变为倍(纵坐标不变),则所得到的图像的函数解析式为 .(2)要得到函数的图像,只需将函数的图像上所有的点1111 .(3)若函数的部分图像如下图所示,则和的值分别是 . 例 1(3) 例 1(4)(4)如图所示,某地夏天 8~14 时用电量变化曲线近似满足函数.① 这一天的最大用电量为______________,最小用电量为 .② 这段曲线的函数解析式为 . 【例 2】已知函数图像的一个最高点(2,),由这个最高点到相邻最低点的图像与轴交于点(6,0),试求函数解析式.【例 3】若函数表示一个振动量: (1)求这个振动的振幅、周期、初相; (2)用“五点法”作出它在一个周期内的图像; (3)说明的图像可由的图像经过怎样的变换而得到.课堂小结三、课后作业1.已知简谐运动的图像经过点(0,1),则该简谐运动的最小正周期和初相分别为 .2 . 电 流 强 度随 时 间变 化 的 函 数的 图 像如右图所示,则当时,电流强度是 .3.如右图,它表示电流在一个周期内的图像,则的解析式为 .4 . 为 ...