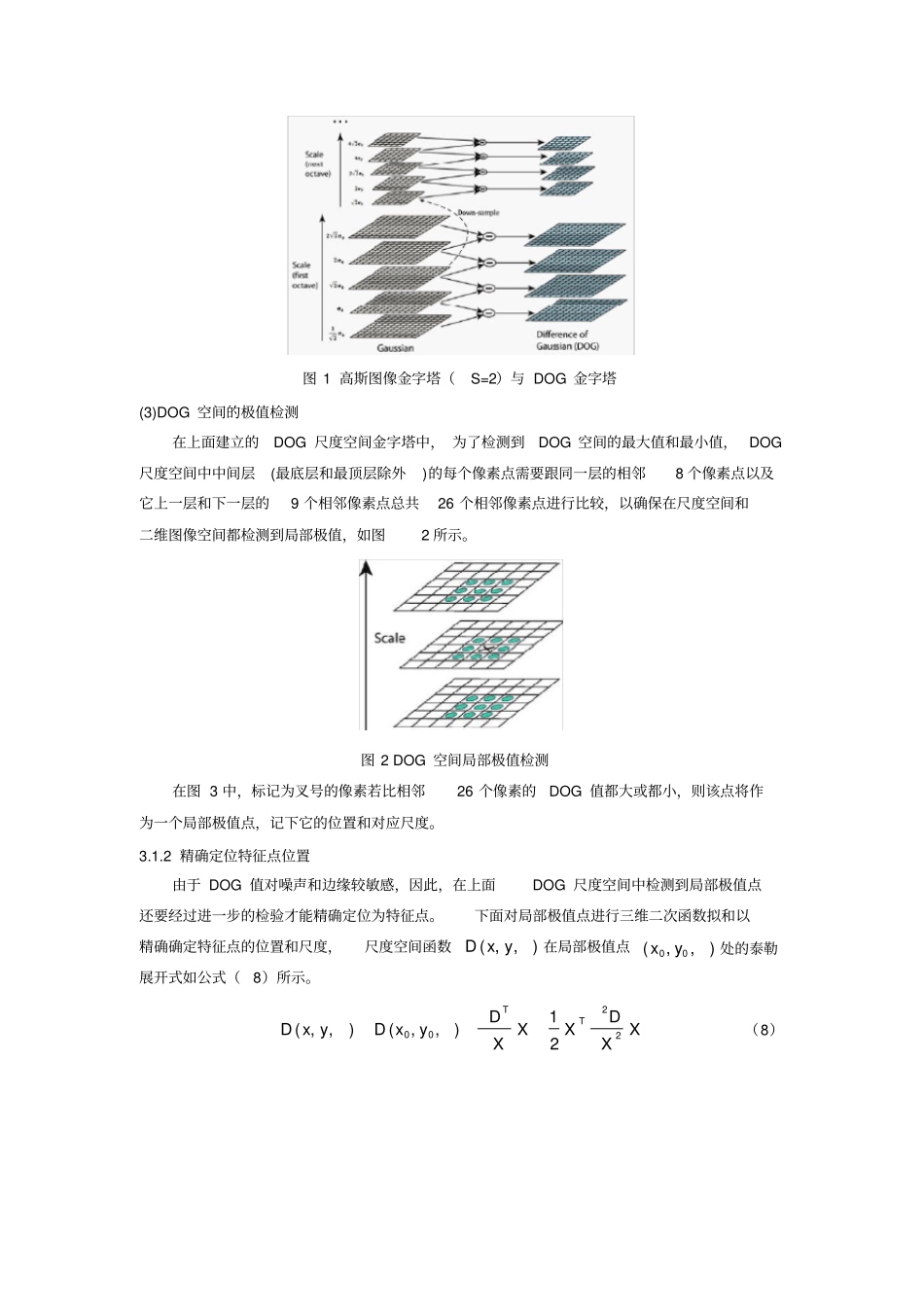
3.1.1 尺度空间极值检测尺度空间理论最早出现于计算机视觉领域,当时其目的是模拟图像数据的多尺度特征。随后 Koendetink 利用扩散方程来描述尺度空间滤波过程,并由此证明高斯核是实现尺度变换的唯一变换核。Lindeberg,Babaud 等人通过不同的推导进一步证明高斯核是唯一的线性核。因此, 尺度空间理论的主要思想是利用高斯核对原始图像进行尺度变换,获得图像多尺度下的尺度空间表示序列,对这些序列进行尺度空间特征提取。二维高斯函数定义如下:222()/221( , ,)2xyG x ye(5)一幅二维图像,在不同尺度下的尺度空间表示可由图像与高斯核卷积得到:( , ,( , ,)*( ,)L x yG x yI x y(6)其中 (x,y)为图像点的像素坐标,I(x,y)为图像数据 , L 代表了图像的尺度空间。σ 称为尺度空间因子, 它也是高斯正态分布的方差,其反映了图像被平滑的程度,其值越小表征图像被平滑程度越小,相应尺度越小。大尺度对应于图像的概貌特征,小尺度对应于图像的细节特征。因此,选择合适的尺度因子平滑是建立尺度空间的关键。在这一步里面,主要是建立高斯金字塔和DOG(Difference of Gaussian) 金字塔,然后在DOG 金字塔里面进行极值检测,以初步确定特征点的位置和所在尺度。(1)建立高斯金字塔为了得到在不同尺度空间下的稳定特征点,将图像( , )I x y 与不同尺度因子下的高斯核( , ,)G x y进行卷积操作,构成高斯金字塔。高斯金字塔有o 阶,一般选择4 阶,每一阶有s 层尺度图像, s 一般选择 5 层。在高斯金字塔的构成中要注意,第 1 阶的第 l 层是放大 2 倍的原始图像, 其目的是为了得到更多的特征点;在同一阶中相邻两层的尺度因子比例系数是k ,则第 1 阶第 2 层的尺度因子是k,然后其它层以此类推则可;第2 阶的第 l 层由第一阶的中间层尺度图像进行子抽样获得,其尺度因子是2k,然后第2 阶的第 2 层的尺度因子是第1 层的 k 倍即3k。第 3 阶的第 1层由第 2 阶的中间层尺度图像进行子抽样获得。其它阶的构成以此类推。(2)建立 DOG 金字塔DOG 即相邻两尺度空间函数之差,用( , ,)D x y来表示,如公式(3)所示:( , ,)(( , ,)( , ,))*( , )( , ,)( , ,)D x yG x y kG x yI x yL x y kL x y(7) DOG 金字塔通过高斯金字塔中相邻尺度空间函数相减即可,如图1 所示。在图中,DOG 金字塔的第l 层的尺度因子与高斯金字塔的第l 层是一致的,其它阶...