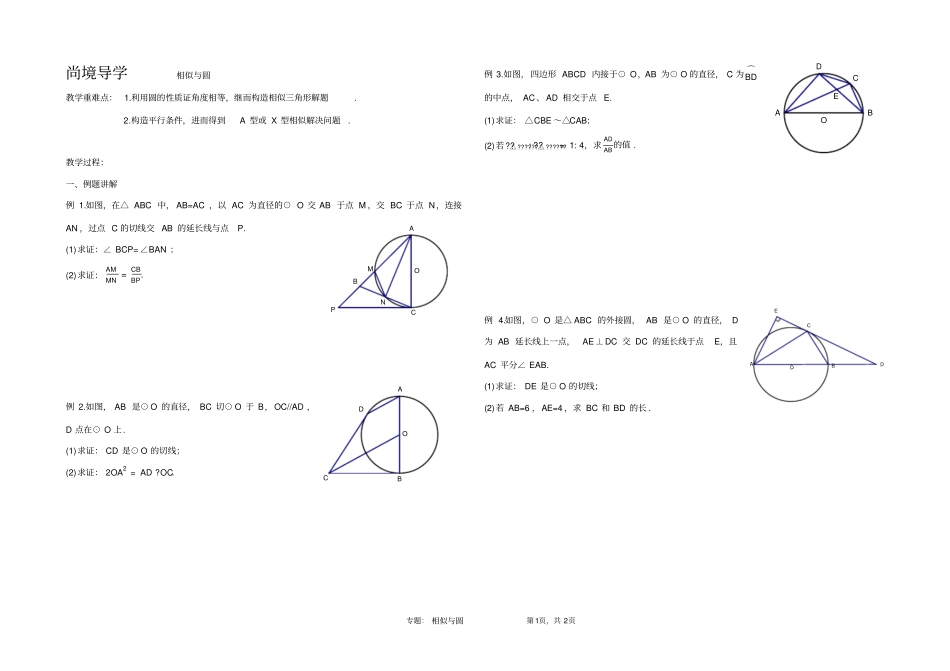
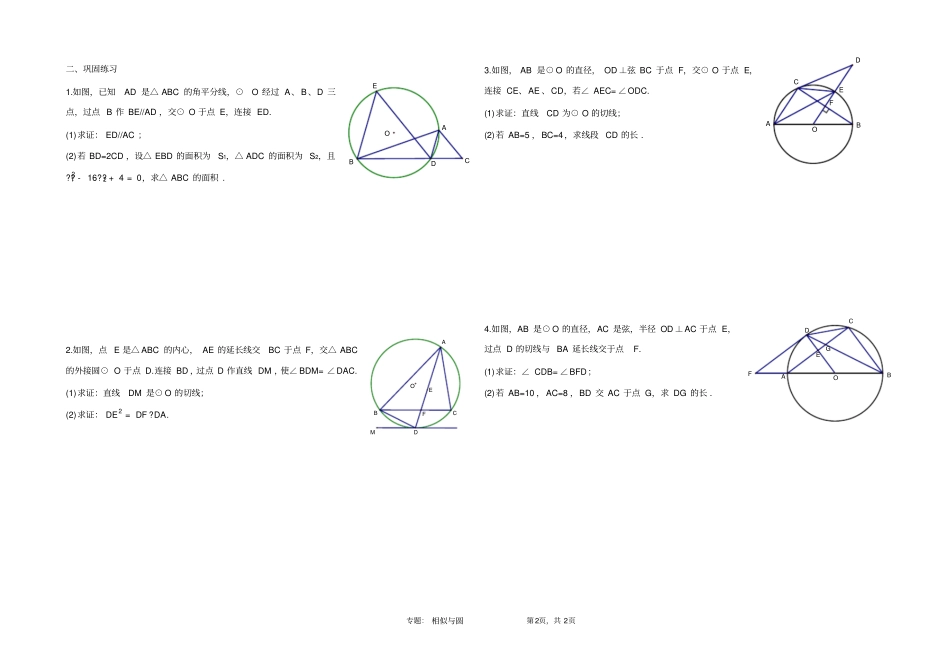
专题: 相似与圆第 1页,共 2页尚境导学相似与圆教学重难点: 1.利用圆的性质证角度相等,继而构造相似三角形解题. 2.构造平行条件,进而得到A 型或 X 型相似解决问题. 教学过程:一、例题讲解例 1.如图,在△ ABC 中, AB=AC ,以 AC 为直径的⊙ O 交 AB 于点 M ,交 BC 于点 N,连接AN ,过点 C 的切线交 AB 的延长线与点P. (1)求证:∠ BCP= ∠BAN ;(2)求证:AMMN =CBBP.例 2.如图, AB 是⊙ O 的直径, BC 切⊙ O 于 B,OC//AD ,D 点在⊙ O 上. (1)求证: CD 是⊙ O 的切线;(2)求证: 2OA2 = AD ?OC.例 3.如图,四边形 ABCD 内接于⊙ O,AB 为⊙ O 的直径, C 为 ⌒BD的中点, AC、AD 相交于点 E. (1)求证: △CBE ~△CAB;(2)若??△ ??????: ??△ ??????= 1: 4,求ADAB 的值 .例 4.如图,⊙ O 是△ ABC 的外接圆, AB 是⊙ O 的直径, D为 AB 延长线上一点,AE⊥DC 交 DC 的延长线于点E,且AC 平分∠ EAB. (1)求证: DE 是⊙ O 的切线;(2)若 AB=6 ,AE=4 ,求 BC 和 BD 的长 .MNBOPCACOBADECOABDEOCBAD专题: 相似与圆第 2页,共 2页二、巩固练习1.如图,已知AD 是△ ABC 的角平分线,⊙O 经过 A、B、D 三点,过点 B 作 BE//AD ,交⊙ O 于点 E,连接 ED. (1)求证: ED//AC ;(2)若 BD=2CD ,设△ EBD 的面积为S1,△ ADC 的面积为 S2,且??12 -16??2 + 4 = 0,求△ ABC 的面积 .2.如图,点 E 是△ ABC 的内心, AE 的延长线交BC 于点 F,交△ ABC的外接圆⊙ O 于点 D.连接 BD ,过点 D 作直线 DM ,使∠ BDM= ∠DAC. (1)求证:直线DM 是⊙ O 的切线;(2)求证: DE2 = DF ?DA. 3.如图, AB 是⊙ O 的直径, OD ⊥弦 BC 于点 F,交⊙ O 于点 E,连接 CE、AE 、CD,若∠ AEC= ∠ODC. (1)求证:直线CD 为⊙ O 的切线;(2)若 AB=5 ,BC=4,求线段 CD 的长 .4.如图,AB 是⊙ O 的直径,AC 是弦,半径 OD ⊥AC 于点 E,过点 D 的切线与 BA 延长线交于点F. (1)求证:∠ CDB= ∠BFD;(2)若 AB=10 ,AC=8 ,BD 交 AC 于点 G,求 DG 的长 .EOABDCGEFDOABCFDEOBCAMEFDOABC