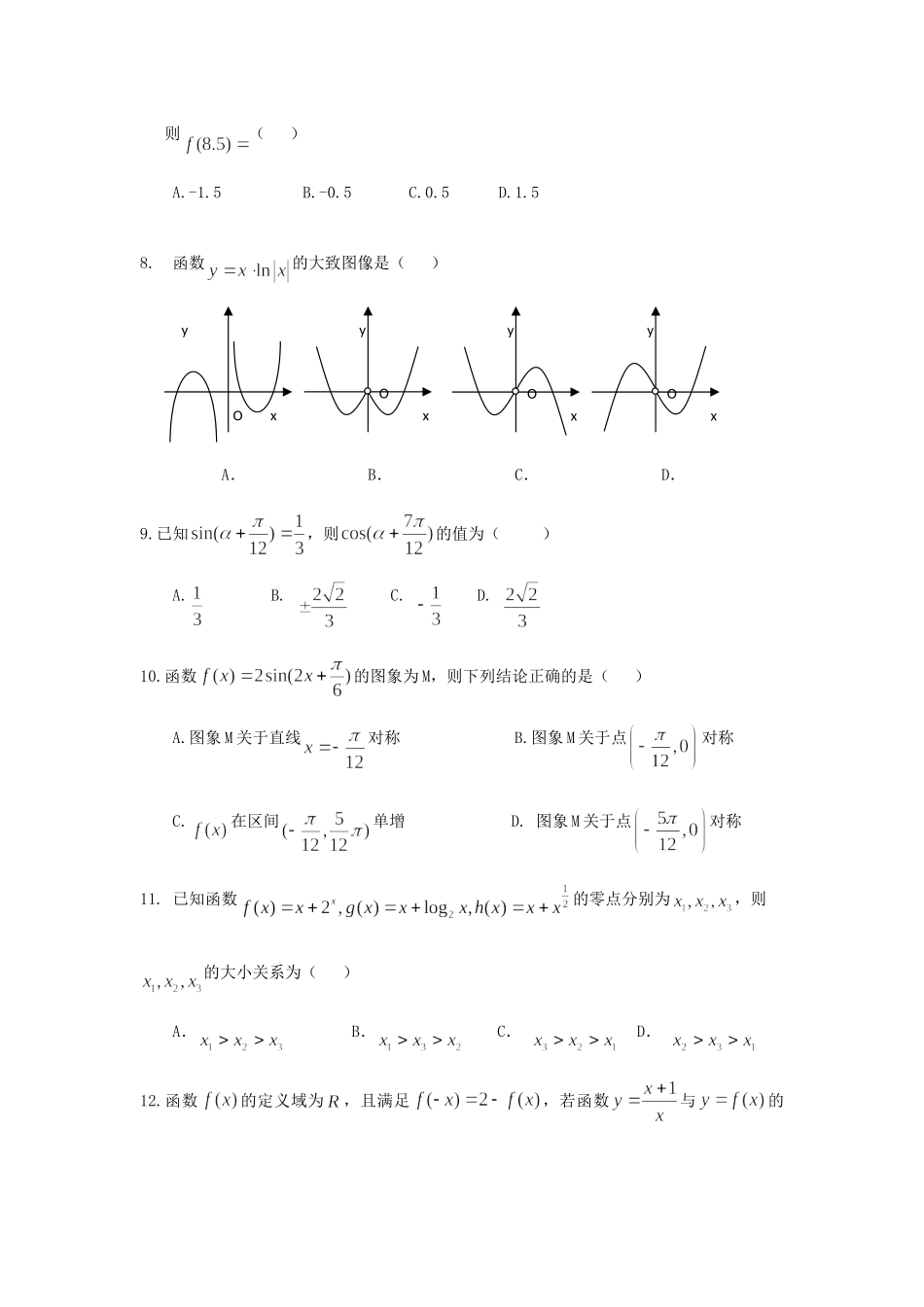
重庆第二外国语学校高 2021 级高一上期第二次质量检测数学试题考试时间:120 分钟 总分:150 分一、选择题(本大题共 12 小题,每小题 5 分,共 60 分.)1 . 全 集,, 则( )A. B. C. D. 2. 已知且为二象限角,则的值为( )A. B. C. D. 3. 函数的最小正周期为( )A. B. C. D. 4. 在用二分法求方程在的近似根的过程中得到,则方程的根落在区间( ) A. B. C. D. 不能确定5.若,,,则( ) A. B. C. D.6.已知 tan2 ,则( )A. 45 B. 54 C. 34 D. 437. 已知是定义在 R 上的偶函数,且满足, 当,则( )A.-1.5 B.-0.5 C.0.5 D.1.58. 函数的大致图像是( ) A.B. C. D.9.已知,则的值为( )A. B. C. D. 10.函数的图象为 M,则下列结论正确的是( )A.图象 M 关于直线对称 B.图象 M 关于点对称C.在区间单增 D. 图象 M 关于点对称11. 已知函数的零点分别为,则的大小关系为( )A. B. C. D. 12.函数的定义域为,且满足,若函数与的xyOxyOxyOxyO图象交于个点分别为,则( )A.0 B. C. D. 二、填空题(本大题共 4 小题,每小题 5 分,共 20 分,请将答案填在答题卡相应位置.)13.已知幂函数过点,则 .14. 已知扇形的半径与弧长相等,且周长的数值是面积的数值的 2 倍,则扇形的半径为 .15. 函数的单调递增区间是 .16. 在中,已知,则 .三、解答题(本大题共 6 小题,共 75 分,解答应写出文字说明,证明过程或演算步骤.)17. (本题满分 10 分)已知,且(1)求的值; (2)求的值. 18. (本题满分 12 分)已知集合(1)若,求; (2)若,求的取值范围.19. (本题满分 12 分)已知(1)用五点作图法在给定坐标系中作出在区间的草图;(先列表后作图)(2)求函数的单调递增区间.20. 已知,.(1)求的值域;(2)记函数的最小值为,求的解析式.21.(本题满分 12 分)某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量(单位:微克)与时间 (单位:小时)之间近似满足如图所示的曲线.(1)写出第一次服药后与 之间的函数关系式;(2)据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到,参考数据:)22. (本题满分 12 分)设函数,(1)若不等式在内恒成立,求的取值范...