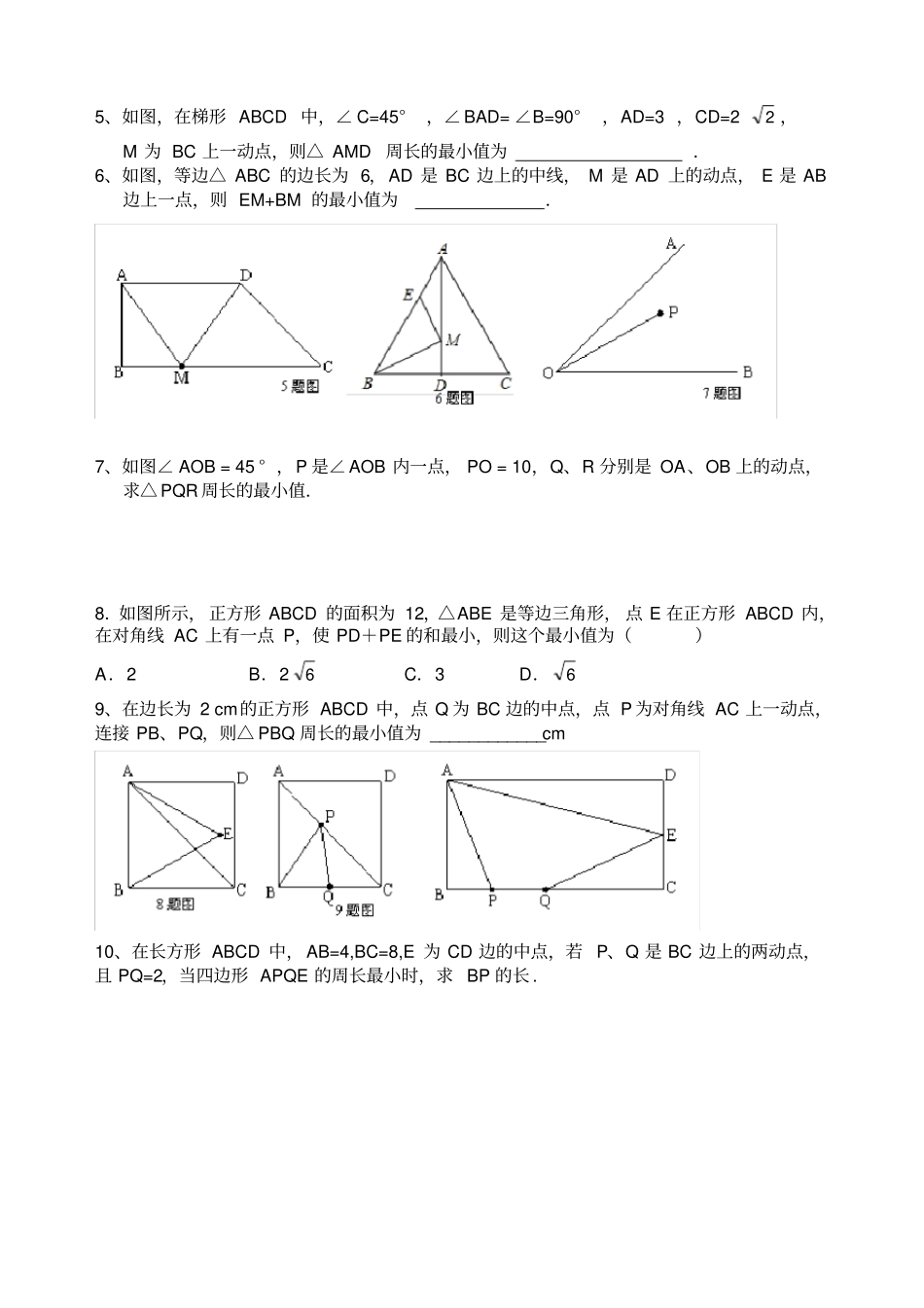
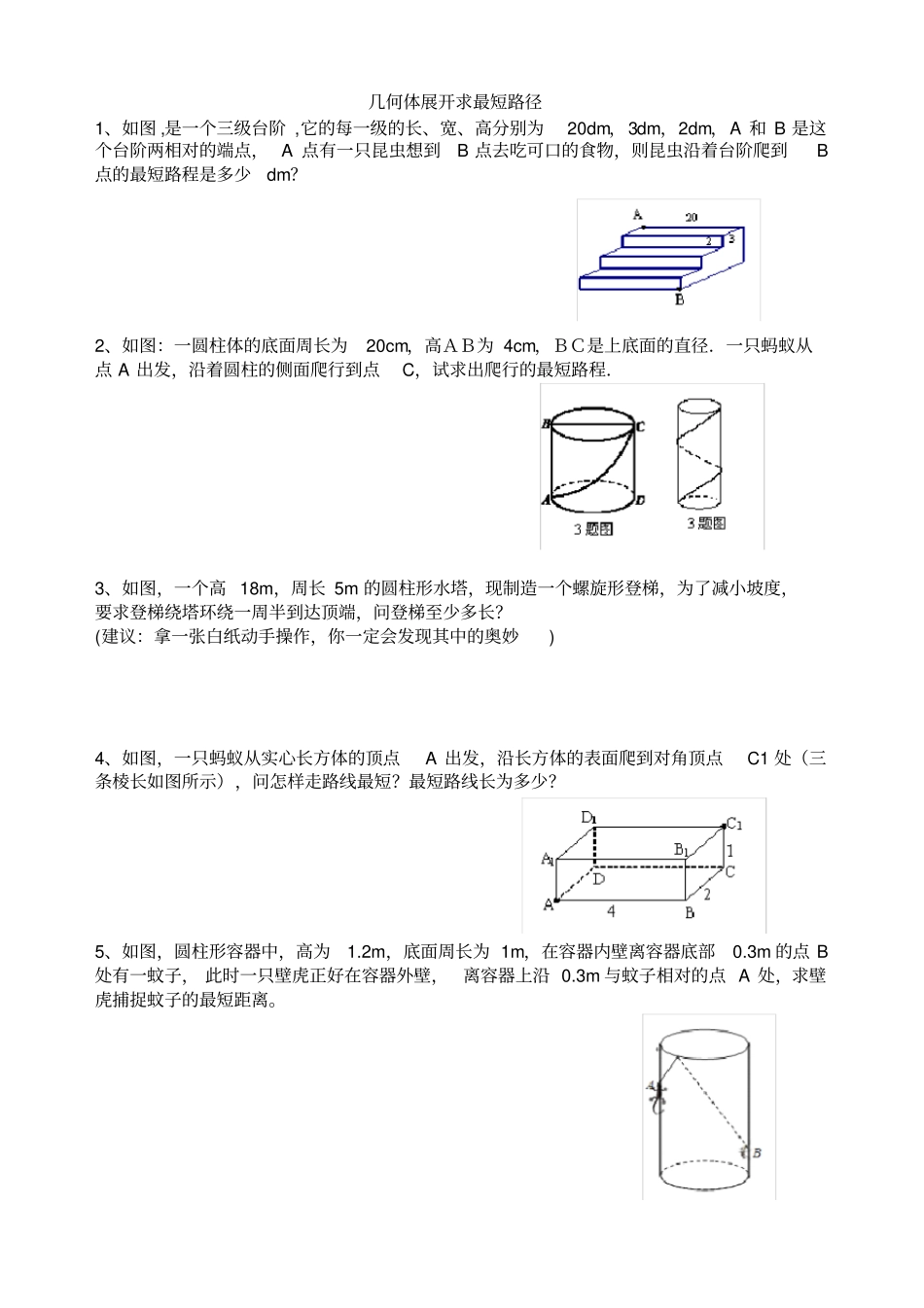
勾股定理练习 (根据对称求最小值 ) 基本模型: 已知点 A、B 为直线m 同侧的两个点, 请在直线 m 上找一点 M,使得 AM+BM有最小值。1、已知边长为 4 的正三角形 ABC 上一点 E,AE=1,AD⊥BC 于 D,请在 AD 上找一点 N,使得 EN+BN 有最小值,并求出最小值。2、.已知边长为 4 的正方形 ABCD 上一点 E,AE=1,请在对角线 AC 上找一点 N,使得 EN+BN 有最小值,并求出最小值。3、如图,已知直线a∥b,且 a 与 b 之间的距离为 4,点 A 到直线 a 的距离为 2,点 B 到直线 b 的距离为 3,AB=230 .试在直线 a 上找一点 M ,在直线 b 上找一点 N,满足MN ⊥a 且 AM+MN+NB的长度和最短,则此时AM+NB= ()A.6 B.8 C.10 D.12 4、已知 AB=20,DA ⊥ AB 于点 A,CB⊥AB 于点 B,DA=10,CB=5.(1)在 AB 上找一点 E,使 EC=ED,并求出 EA 的长;(2)在 AB 上找一点 F,使 FC+FD 最小,并求出这个最小值5、如图,在梯形 ABCD 中,∠ C=45°,∠ BAD= ∠B=90°,AD=3 ,CD=2 2 ,M 为 BC 上一动点,则△ AMD 周长的最小值为.6、如图,等边△ ABC 的边长为 6,AD 是 BC 边上的中线, M 是 AD 上的动点, E 是 AB边上一点,则 EM+BM 的最小值为.7、如图∠ AOB = 45 ° ,P 是∠ AOB 内一点, PO = 10,Q、R 分别是 OA、OB 上的动点,求△ PQR 周长的最小值.8.如图所示, 正方形 ABCD 的面积为 12,△ABE 是等边三角形, 点 E 在正方形 ABCD 内,在对角线 AC 上有一点 P,使 PD+PE 的和最小,则这个最小值为()A.2 B.2 6C.3 D.69、在边长为 2 cm的正方形 ABCD 中,点 Q 为 BC 边的中点,点 P 为对角线 AC 上一动点,连接 PB、PQ,则△ PBQ 周长的最小值为 ____________cm 10、在长方形 ABCD 中, AB=4,BC=8,E 为 CD 边的中点,若 P、Q 是 BC 边上的两动点,且 PQ=2,当四边形 APQE 的周长最小时,求 BP 的长 . 几何体展开求最短路径1、如图 ,是一个三级台阶 ,它的每一级的长、宽、高分别为20dm,3dm,2dm,A 和 B 是这个台阶两相对的端点, A 点有一只昆虫想到B 点去吃可口的食物,则昆虫沿着台阶爬到B点的最短路程是多少dm?2、如图:一圆柱体的底面周长为20cm,高AB为 4cm,BC是上底面的直径.一只蚂蚁从点 A 出发,沿着圆柱的侧面爬行到点C...