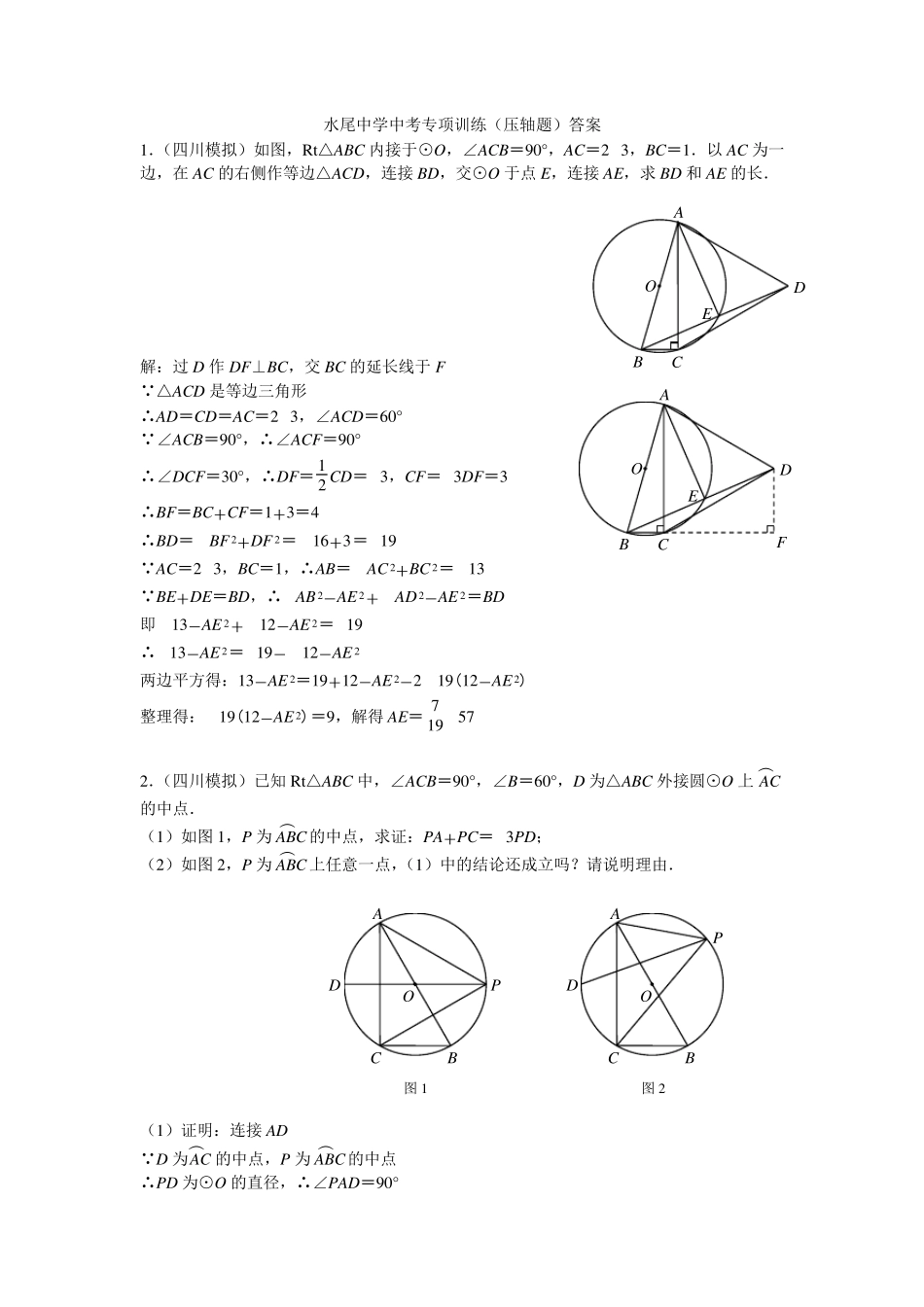
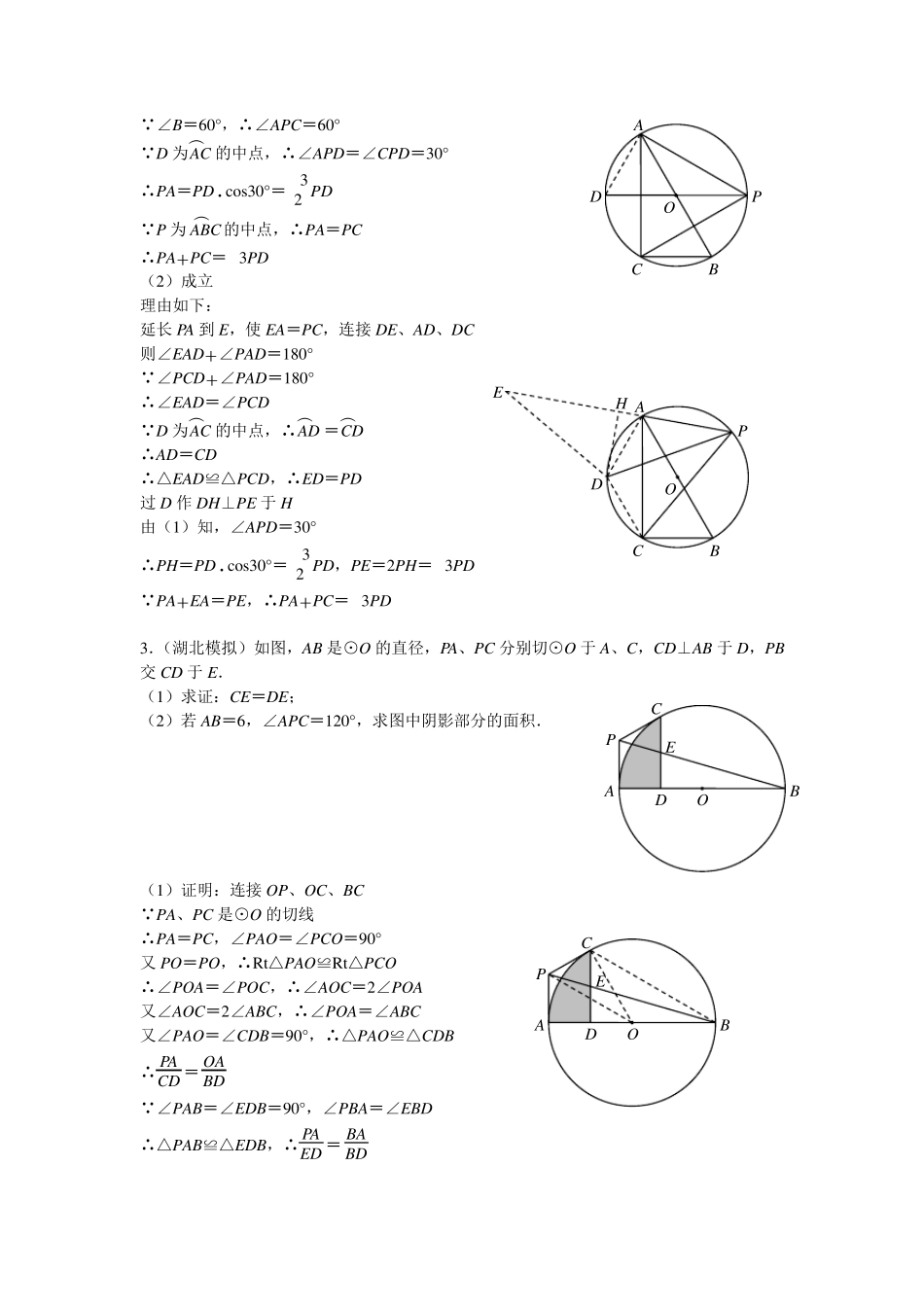
水尾中学中考专项训练(压轴题)答案 1.(四川模拟)如图,Rt△ABC 内接于⊙O,∠ACB=90°,AC=2 3,BC=1.以 AC 为一边,在 AC 的右侧作等边△ACD,连接BD,交⊙O 于点 E,连接AE,求 BD 和 AE 的长. 解:过 D 作 DF⊥BC,交 BC 的延长线于F △ACD 是等边三角形 ∴AD=CD=AC=2 3,∠ACD=60° ∠ACB=90°,∴∠ACF=90° ∴∠DCF=30°,∴DF= 1 2 CD=3,CF=3DF=3 ∴BF=BC+CF=1+3=4 ∴BD= BF 2+DF 2 = 16+3 =19 AC=2 3,BC=1,∴AB= AC 2+BC 2 = 13 BE+DE=BD,∴AB 2-AE 2 + AD 2-AE 2 =BD 即 13-AE 2 + 12-AE 2 =19 ∴13-AE 2 =19- 12-AE 2 两边平方得:13-AE 2=19+12-AE 2-2 19(12-AE 2) 整理得:19(12-AE 2) =9,解得 AE= 7 19 57 2.(四川模拟)已知 Rt△ABC 中,∠ACB=90°,∠B=60°,D 为△ABC 外接圆⊙O 上 AC︵ 的中点. (1)如图1,P为 ABC︵ 的中点,求证:PA+PC=3PD; (2)如图2,P为 ABC︵ 上任意一点,(1)中的结论还成立吗?请说明理由. (1)证明:连接AD D 为AC︵ 的中点,P为 ABC︵ 的中点 ∴PD 为⊙O 的直径,∴∠PAD=90° A B D C E O A B D C E O F D A P O C B 图1 D A P O C B 图2 ∠B=60°,∴∠APC=60° D 为AC︵ 的中点,∴∠APD=∠CPD=30° ∴PA=PD·cos30°= 3 2 PD P为 ABC︵ 的中点,∴PA=PC ∴PA+PC=3PD (2)成立 理由如下: 延长 PA 到 E,使 EA=PC,连接 DE、AD、DC 则∠EAD+∠PAD=180° ∠PCD+∠PAD=180° ∴∠EAD=∠PCD D 为AC︵ 的中点,∴AD︵ =CD︵ ∴AD=CD ∴△EAD≌△PCD,∴ED=PD 过 D 作 DH⊥PE 于 H 由(1)知,∠APD=30° ∴PH=PD·cos30°= 3 2 PD,PE=2PH=3PD PA+EA=PE,∴PA+PC=3PD 3.(湖北模拟)如图,AB 是⊙O 的直径,PA、PC 分别切⊙O 于 A、C,CD⊥AB 于 D,PB交 CD 于 E. (1)求证:CE=DE; (2)若 AB=6,∠APC=120°,求图中阴影部分的面积. (1)证明:连接 OP、OC、BC PA、PC 是⊙O 的切线 ∴PA=PC,∠PAO=∠PCO=90° 又 PO=PO,∴Rt△PAO≌Rt△PCO ∴∠POA=∠POC,∴∠AOC=2∠POA 又∠AOC=2∠ABC,∴∠POA=∠ABC 又∠PAO=∠CDB=90°,∴△P...