10理论力学VIP免费

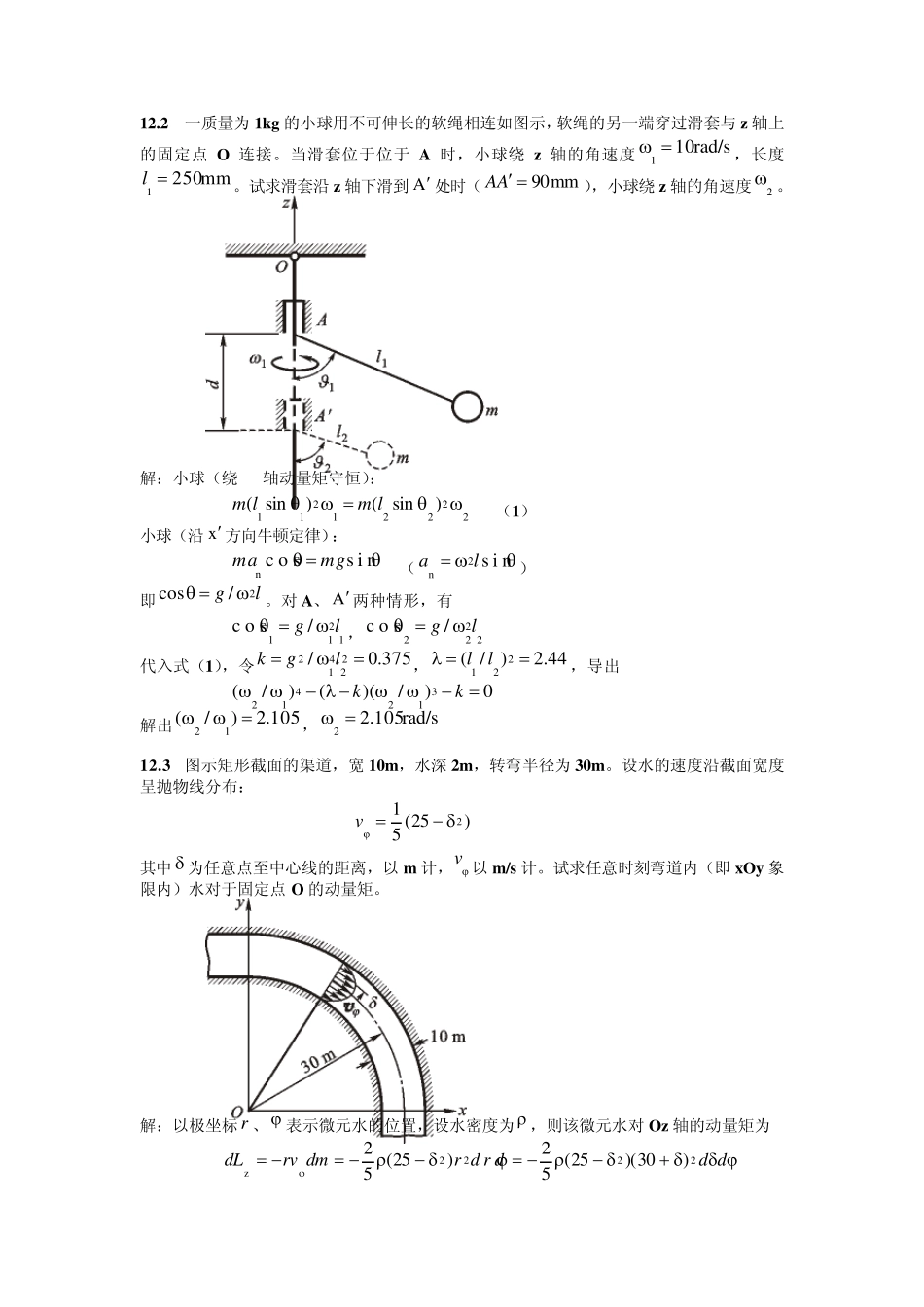
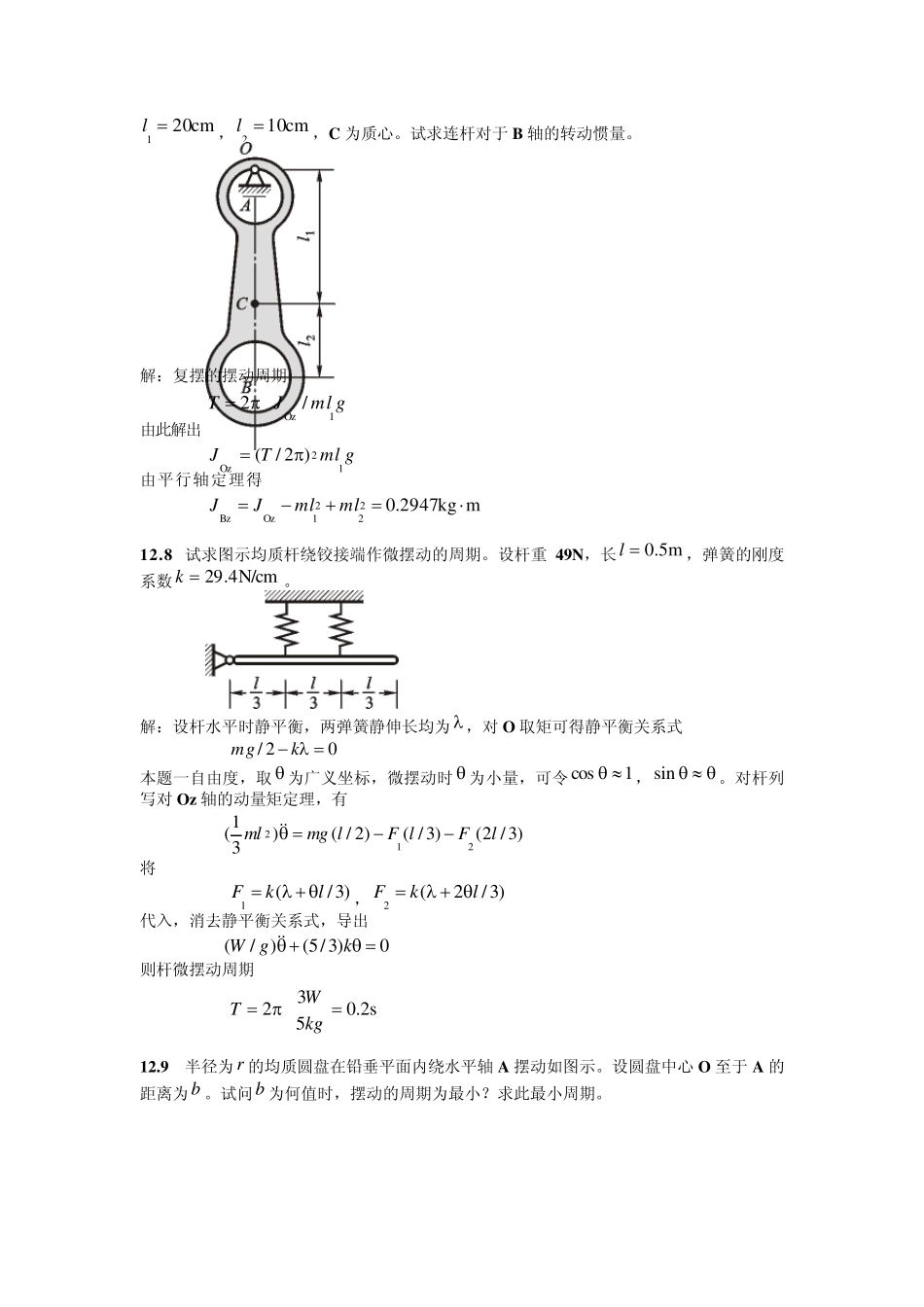
12.2 一质量为1kg 的小球用不可伸长的软绳相连如图示，软绳的另一端穿过滑套与z 轴上的固定点O 连接。当滑套位于位于A 时，小球绕z 轴的角速度 rad/s101 ，长度mm2501 l。试求滑套沿z 轴下滑到A 处时（mm90AA），小球绕z 轴的角速度2 。 解：小球（绕Oz轴动量矩守恒）： 22221211)sin()sin(lmlm （1） 小球（沿x 方向牛顿定律）： s i nc o snmgma （s i n2nla） 即lg2/cos。对A、 A 两种情形，有 1211/c o slg ，2222/c o slg  代入式（1），令375.0/22412lgk，44.2)/(221ll，导出 0)/)(()/(312412kk 解出105.2)/(12，rad/s105.22  12.3 图示矩形截面的渠道，宽 10m，水深 2m，转弯半径为30m。设水的速度沿截面宽度呈抛物线分布： )25(512v 其中  为任意点至中心线的距离，以 m 计，v 以 m/s 计。试求任意时刻弯道内（即xOy 象限内）水对于固定点O 的动量矩。 解：以极坐标 r 、  表示微元水的位置，设水密度为 ，则该微元水对Oz 轴的动量矩为 ddd r drdmrvdL2222z)30)(25(52)25(52 弯道内水对固定点O 的动量矩沿Oz 轴，即 smN1048.9)3.150833(5|)5/3/87522500(52)30)(25(5272/055532/05522zdddL 12.4 试求厚度不计的图示中空均质圆盘对于直径轴的转动惯量。 解：设中空圆盘单位面积质量为 ，则有 )(41))((41)(41)(4121222122212221212222xRRmRRRRRRRRJ 式中m 为中空圆盘的质量。 12.5 试计算图示均质半圆薄板对于x 轴的转动惯量。 解：引入过 O 点平行于x 轴的坐标轴x’，则关于x’轴的转动惯量为 2x41 mrJ 由平行轴移轴定理，关于过 C 点的平行于x 的轴的惯量为 222xx)91641()34(CmrrmJJ 而关于坐标轴x 的惯量则为 22xx)3845()34(CmrrrmJJ 12.6 试计算均质半圆球对于过质心且平行于其底面的任意轴的转动惯量。 解：均质半圆球关于其底面的任意轴的转动惯量为 2x52 mrJ  由于质心距底面的高度为 rzc83 因此，均质半圆球对于过质心且平行于的任意轴的转动惯量为 22xx3 2 083)83(CmrrmJJ 12.7 测得图示连杆 AB 绕 O ...