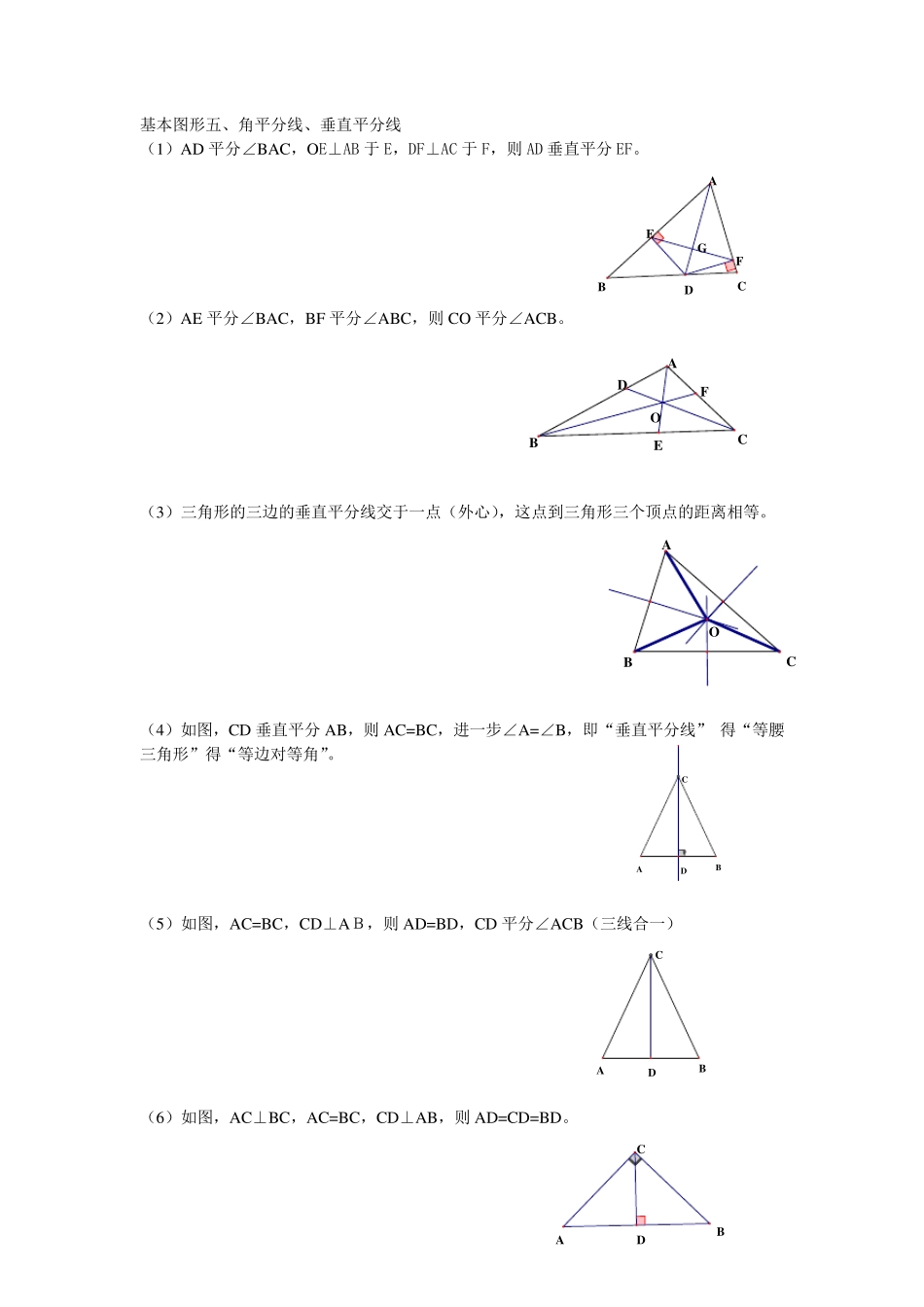
八年级(上)几何基本图形及结论 基本图形一、蝶形(对顶三角形) 如图1,AB、CD 交于O,则:∠A+∠C=∠B+∠D; 若∠A=∠D,则∠C=∠B 基本图形二、 如图2,△ABC 中,AD 为高,AE 为角平分线, 则∠DAE = 12 (∠B-∠C) 基本图形三、 (1)如图,在△ABC 中,∠B、∠C 的平分线相交于P点,则∠P=_____________. (2)如图,在△ABC 中,∠B、∠ACB 的外角平分线相交于P点,则∠P=_____________. (3) 如图,在△ABC 中,∠B、∠C 的外角平分线相交于P点,则∠P=_____________. 基本图形四、“垂直且相等” (1)如图①、②,AC⊥BC,且 AC=BC,AD⊥MN 于D,BE⊥MN 于E,则AD-BE=DE或AD+BE=DE; 图1 图2 (2)如图③、④,AC⊥BC,且 AC=BC,BP⊥MN 于P,CQ⊥MN 于Q,过 C 点向 BP 作 CD⊥BP于D,则AP-BP=2PQ 或 AP+BP=2PQ。 图3 图4 (1)OBDCAEDCBAPCBA(2)DCPBA(1)PCBADEMNCBADEMNCBAQPDMNCBANMPQDCBA基本图形五、角平分线、垂直平分线 (1)AD 平分∠BAC,O E⊥AB 于E,DF⊥AC 于F,则AD 垂直平分EF。 (2)AE 平分∠BAC,BF 平分∠ABC,则CO 平分∠ACB。 (3)三角形的三边的垂直平分线交于一点(外心),这点到三角形三个顶点的距离相等。 (4)如图,CD 垂直平分AB,则AC=BC,进一步∠A=∠B,即“垂直平分线” 得“等腰三角形”得“等边对等角”。 (5)如图,AC=BC,CD⊥AB,则AD=BD,CD 平分∠ACB(三线合一) (6)如图,AC⊥BC,AC=BC,CD⊥AB,则AD=CD=BD。 GFEDCBAOFDECBAOCBADBCADBCADBCA基本图形六、中点问题 (1)如图,AC=BC,∠ACB=90°,O 为斜边 AB 的中点,D 为 AC 上任一点,DO⊥OE,则 ①OD=OE,②AD+BE=AC,③△DOE 为等腰直角三角形;④S四边形CDEO= 12 S△ACB (2)如图,AC=BC,∠ACB=90°,CD⊥AB 于 D,AG⊥CE 于 G,则 DF=DE,若 E 为 AB 延长线上一点,结论仍成立。 基本图形七、垂线段、距离、面积: (1)如图,等腰三角形底边上任意一点到两腰的距离和等于腰上的高;(面积法) (2)底边延长线上一点到两腰的距离之差等于一腰上的高。(面积法) 基本图形八、Rt△、斜三角形中的特殊边角关系 (1)如图,∠ACB=90°,∠B=30°,CD⊥AB 于 D,则 AB=4AD,BD=3AD; (2)等腰三角形一腰上的高等于腰长的一半,则底角为__________________。 EDOBCAFGEDBCAGFEDCBAGFEDCBA30°BDCABDCADCBA基本图形九、...