极坐标详细讲解VIP免费

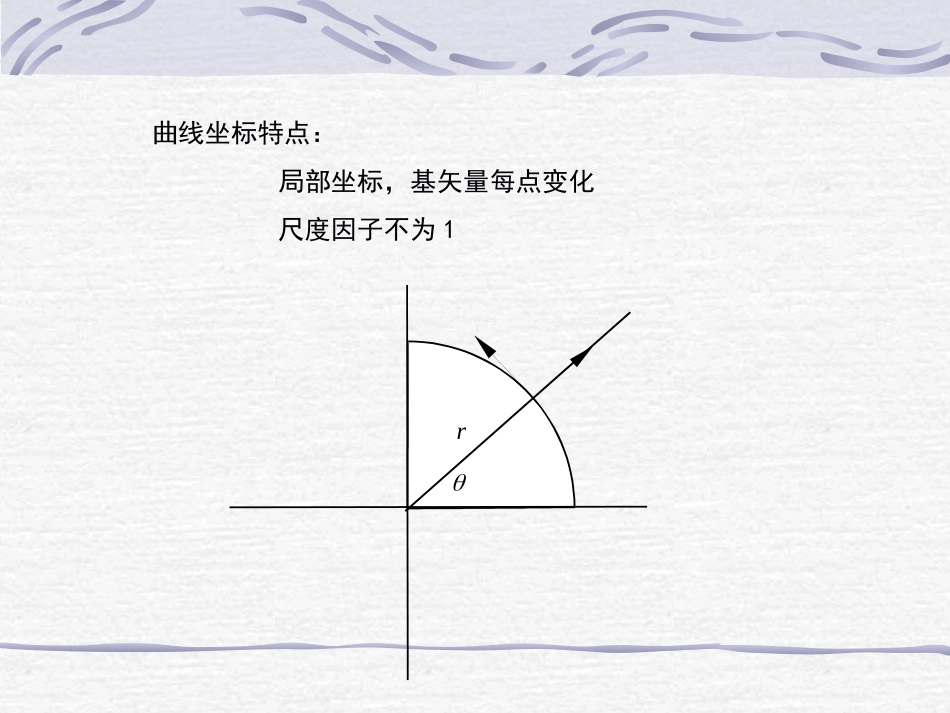
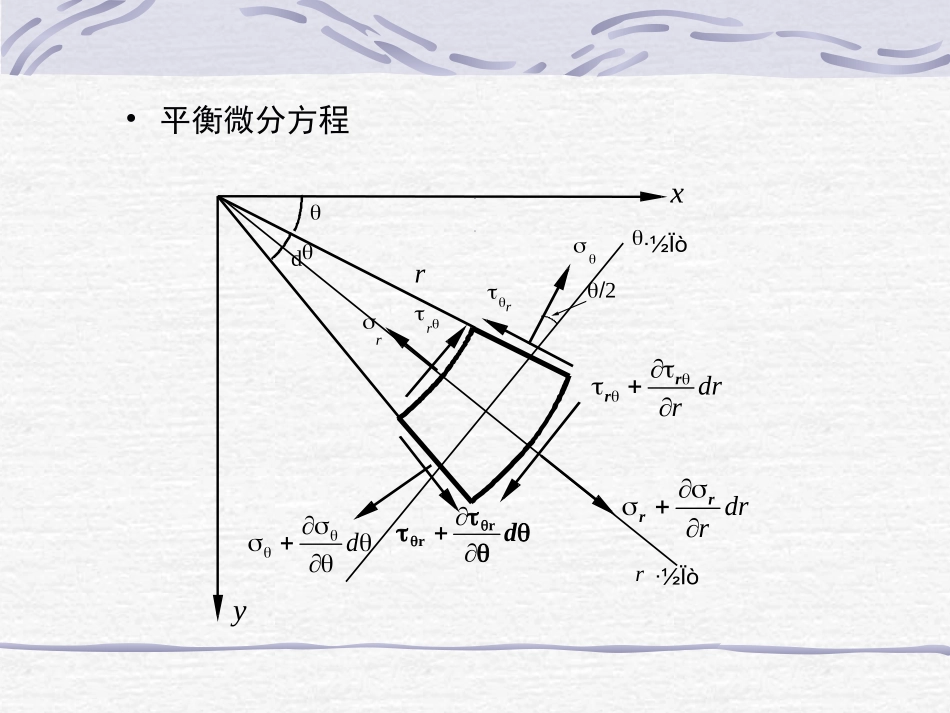
极坐标解平面问题必要性：对于特殊几何形状和受力分布的情况，可使求解简单特点：方程形式将改变，但物理本质应不变方法：通过张量分量的坐标变换；使用物理定律，直接推导；r曲线坐标特点：局部坐标，基矢量每点变化尺度因子不为1dryxrrr·½Ïòr·½Ïòddrrdrrrrdrrrr•平衡微分方程2ddrdrdddrrdrrrrr02drrdkdrdrdddrrrrrddrrdrrdrdrdrr0221rdrdkddrddrdrdrrr径向平衡环向平衡01rrrrKrrr021Krrrrr平衡微分方程BB'PP'AA'drdxyrudrudrruuPAPAA'P'rrrrrrurdθrdθdθruPBB'-PBP'εrrθurrdudθuuBPPP'BB'rrrr1θurr1r仅产生经向位移PBBAAP''''''dyx仅产生环向位移uPPduuBBdrruuAAθθθθurrdθudθθuuBP'PP''BB'BPBP'P''B'1rudrudrruuPA'PP''AA'θθθθru'POP'θrurrurrur1ruruurrrr1几何方程物理方程EErrEErGrr22211222rrrr22＝0变形协调方程21122rrrr22rθrrrθrr222111rqaqb例4-5圆筒内半径为a，外半径为b，内壁作用均匀压力为qa，外壁作用均布压力qb，求应力分布。解：这是一个轴对称问题。当弹性体的几何形状和外荷载为轴对称时，应力与应变也都应是轴对称的，它们仅是r的函数，而与无关。应力函数：=(r)drdσ,drdr22θ1rr=r=0协调方程简化为0)1(2drdrdrd22协调方程的通解是：=Alnr+Br2lnr+Cr2+DCrBrA2)ln21(2rCrBrA2)ln23(2力边界条件：(r)r=a=qa(r)r=b=qb(r)r=a=0(r)r=b=0前面两个边界条件可求出A、C，后两个条件自然满足。sincos)1(2)31()1(ln)1(2)1(1KICrBrrBrrAEurcossin4KIHrEBru使用位移单值条件求常数BPxy例4-6半无限体上受集中力作用，该集中力与水平方向夹角为，求应力分量。解：应用因次分析方法来设应力函数。应力分量的因次是[力]/长度]-2，集中力的因次是[力]/[长度]-1（对空间而言，它是沿厚度方向分布的力），而是无因次的，因此应力分量的表达式应取下面的形式=(P,r,)=rPf()=rf()0)()(2)(122443fdfddfdrf()=Acos+Bsin＋(Ccos+Dsin)(r,)=Arcos+Brsin＋(Crcos+Drsin)代入变形协调方程Arcos+Brsin=Ax+By是线性项，不产生应力sincos211222CDrrrrr022r0)1(rrrr边界条件(r)r0,=/2=0(r)r0,=/2=0自然满足0coscosr22Prd0sinsinr22Prd例4-7如图所示，楔形体两边受均匀分布的切向荷载作用，求其中的应力分布。rxyqqO解：（1）根据因次分析选择并求解=(,q,r,)=r2f()代入协调方程0)(4)(122442dfddfdr通解是：f()=Asin2+Bcos2＋C+D22211rrrr22r)1(rrrr=2Asin22Bcos2＋2C+2D＝2(Asin2+Bcos2＋C+D)=2Acos2+2Bsin2C根据力边界条件求出常数A、B、C、D()==0(r)==q(r)==qA=0，C=0，α2sin2qBαqD2tan2