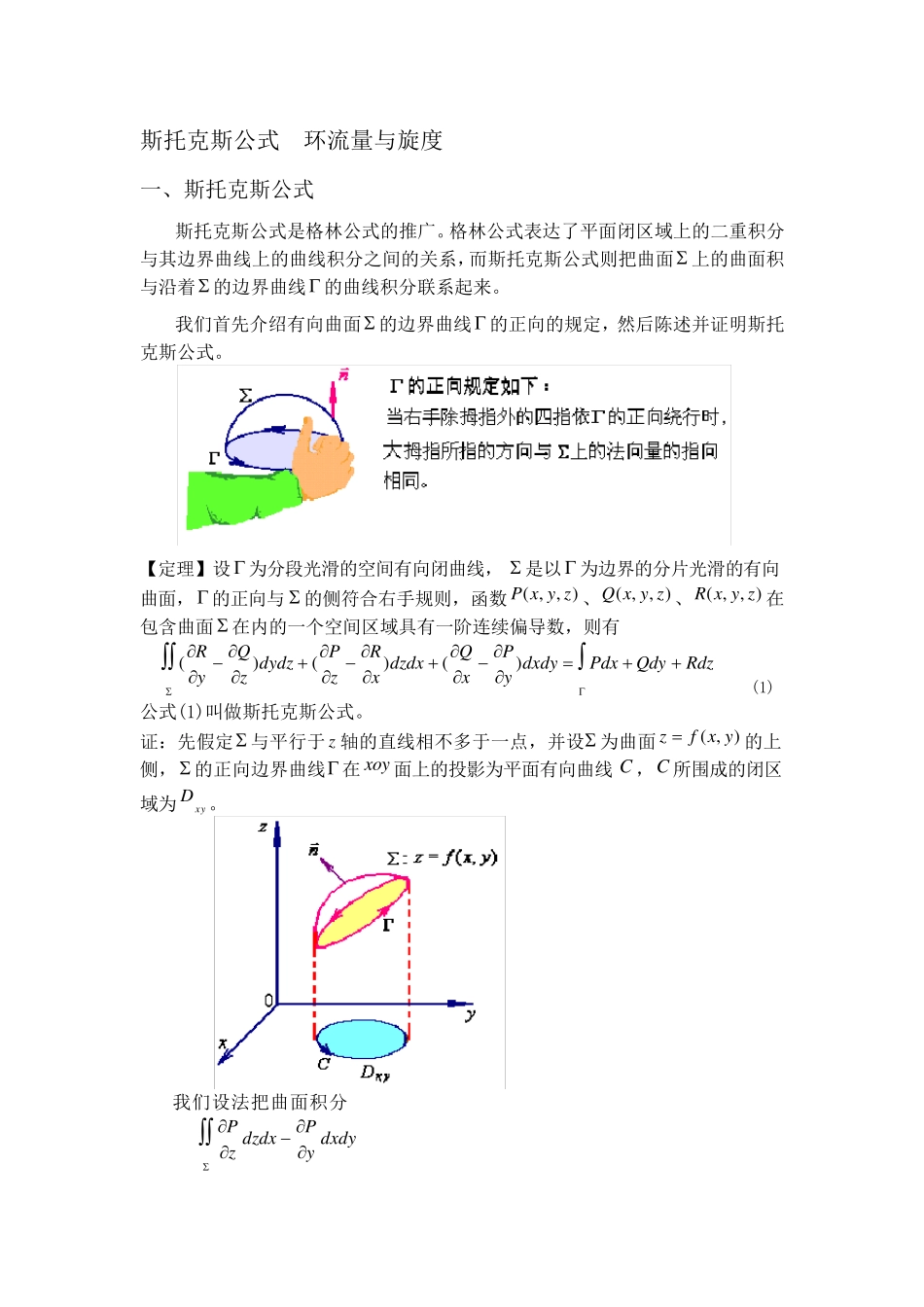
斯托克斯公式 环流量与旋度 一、斯托克斯公式 斯托克斯公式是格林公式的推广。格林公式表达了平面闭区域上的二重积分与其边界曲线上的曲线积分之间的关系,而斯托克斯公式则把曲面 上的曲面积与沿着 的边界曲线 的曲线积分联系起来。 我们首先介绍有向曲面 的边界曲线 的正向的规定,然后陈述并证明斯托克斯公式。 【定理】设 为分段光滑的空间有向闭曲线, 是以 为边界的分片光滑的有向曲面, 的正向与 的侧符合右手规则,函数),,(zyxP、),,(zyxQ、),,(zyxR在包含曲面 在内的一个空间区域具有一阶连续偏导数,则有 RdzQdyPdxdxdyyPxQdzdxxRzPdydzzQyR)()()( (1) 公式(1)叫做斯托克斯公式。 证:先假定 与平行于 z 轴的直线相不多于一点,并设 为曲面),(yxfz 的上侧, 的正向边界曲线 在 xoy 面上的投影为平面有向曲线 C ,C 所围成的闭区域为xyD。 我们设法把曲面积分 dxdyyPdzdxzP 化为闭区域xyD上的二重积分,然后通过格林公式使它与曲线积分联系。 根据对面积的和对坐标的曲面积分间的关系,有 dSyPzPdxdyyPdzdxzP)coscos( (2) 由第 8.6 节知道,有向曲面 的法向量的方向余弦为 221cosyxxfff,221cosyxyfff,2211cosyxff 因此coscosyf,把它代入(2)式得 dSyPfzPdxdyyPdzdxzPycos 即 dSyPfzPdxdyyPdzdxzPycos (3) 上式右端的曲面积分化为二重积分时,应把),,(zyxP中的z 用),(yxf来代替,因为由复合函数的微分法,有 yfzPyPyxfyxPy)],(,,[ 所以,(3)式可写成 xyDdxdyyxfyxPydxdyyPdzdxzP)],(,,[ 根据格林公式,上式右端的二重积分可化为沿闭区域xyD的边界C 的曲线积分 xyDcdxyxfyxPdxdyyxfyxPy)],(,,[)],(,,[ 于是 cdxyxfyxPdxdyyPdzdxzP)],(,,[ 因为函数)],(,,[yxfyxP在曲线C 上点),(yx处的值与函数),,(zyxP在曲线 上对应点),,(zyx处的值是一样的,并且两曲线上的对应小弧段在 x 轴上的投影也是一样,根据曲线积分的定义,上式右端的曲线积分等于曲线 上的曲线积分dxzyx...