球与正三棱锥和正三棱柱的切接关系VIP免费

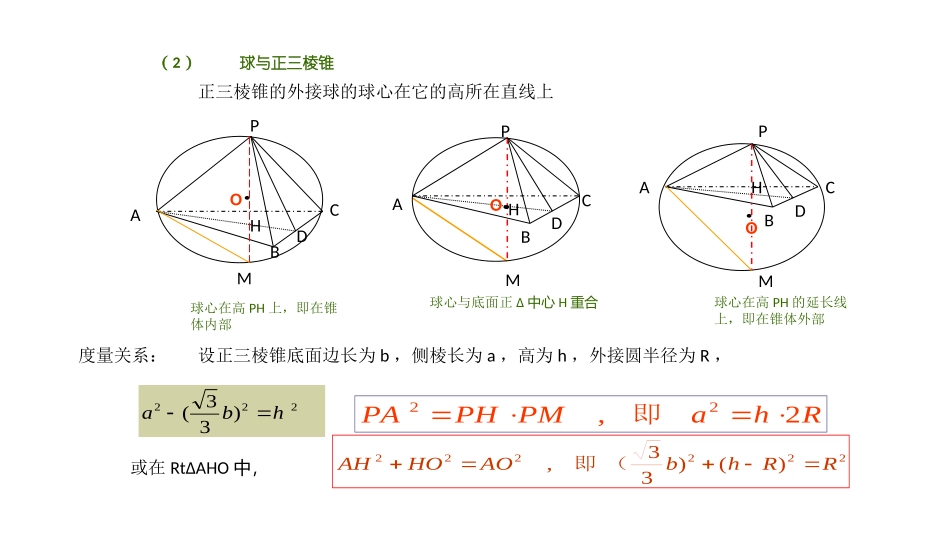
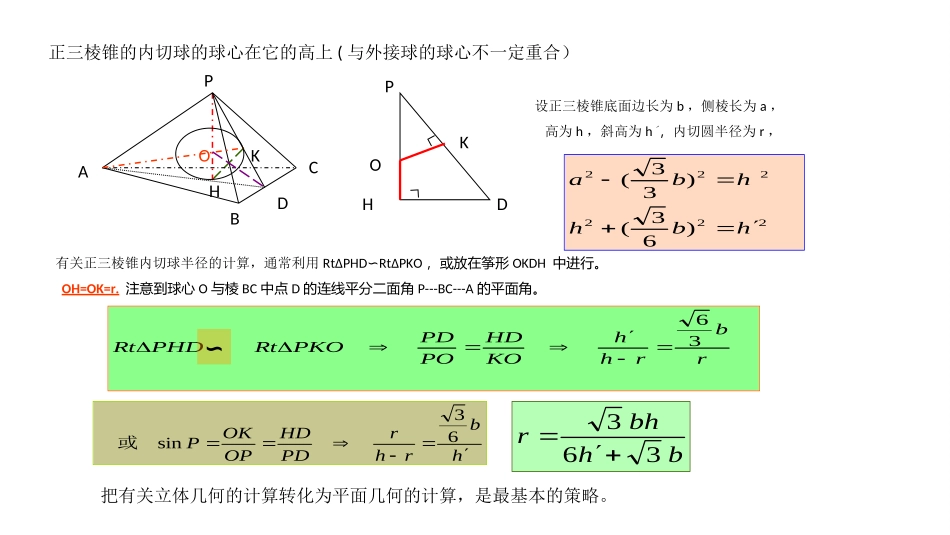
（2）球与正三棱锥OPABCDHMOHPABCDM正三棱锥的外接球的球心在它的高所在直线上球心在高PH上，即在锥体内部球心在高PH的延长线上，即在锥体外部球心与底面正Δ中心H重合OPACDMHB度量关系：设正三棱锥底面边长为b，侧棱长为a，高为h，外接圆半径为R，222)33(hbaRhaPMPHPA2,22即或在RtΔAHO中，222222)()33,RRhbAOHOAH（即OPABCDKH正三棱锥的内切球的球心在它的高上(与外接球的球心不一定重合）有关正三棱锥内切球半径的计算，通常利用RtΔPHDRt∽ΔPKO，或放在筝形OKDH中进行。OH=OK=r.注意到球心O与棱BC中点D的连线平分二面角P---BC---A的平面角。把有关立体几何的计算转化为平面几何的计算，是最基本的策略。PHDOK∟∟rbrhhKOHDPOPDPKORtPHDRt36hbrhrPDHDOPOKP63sin或222222)63()33(hbhhba设正三棱锥底面边长为b，侧棱长为a，高为h，斜高为h́，内切圆半径为r，∽bhbhr363正三棱锥P---ABC的侧棱长为1，底面边长为，它的四个顶点在同一个球面上，则球的体积为（）23622332AH339396122AHPAPHA解：设P在底面ABC上的射影为H，则H为正ΔABC的中心.延长PH交球面于M，则PM为球的一直径，∴∠PAM=90°由RtΔ中的射影定理得：232331,22RRPMPHPA，即2323343433）（球RV6.66.3.23.DCBAOPABCDMH法二由AH>PH知：球心O在正三棱锥的高PH的延长线上。在RtΔAHO,有：23,)33()36(222RRR题目：题目：正三棱锥P—ABC的三条侧棱两两互相垂直，则该正三棱锥的内切球与外接球的半径之比为()解析：OPABCDKHPHDOK∟∟设正三棱锥侧棱长为a，底面边长为b， 三侧棱两两垂直，∴各侧面都是全等的等腰直角三角形。ab2aaabahah3396)33(,222222高斜高bhbhr363代入正三棱锥内切球半径公式：得：aar633333133263323633Rr又正三棱锥外接球半径aR233:)13(.3:)13(.)33(:1.3:1.DCBAD已知三棱锥P—ABC的四个顶点均在半径为1的球面上，且满足PBPAPBPA00PBPA0PCPB0PAPC同理，PBPC,PCPA,⊥⊥即PA、PB、PC两两互相垂直4)2(2222RPCPBPA易知，该三棱锥三个侧面均为RtΔ，所以，其侧面积为2)(21)(21222cbacabcabS解析：222222222,2,2,2cbacabcabcaacbccbabba三式相加得：说明：,,,cPCbPBaPA设则三棱锥的侧面积的最大值为（）41.21.1.2.DCBAA题目：提示：三棱锥三侧面两两垂直三侧棱两两垂直正三棱锥对棱互相垂直，即SB⊥AC,又SB∥MN,且AM⊥MN,所以，SB⊥平面SAC。故，SB⊥SA,SB⊥SC,进而，SA⊥SC.则三侧棱互相垂直。以S为顶点，将三棱锥补成一个正方体，则球的直径设三棱锥的三个侧面两两垂直，且侧棱长均为，则其外接球大圆的面积为（）32SA在正三棱锥S—ABC中，M、N分别是棱SC、BC的中点，且MN⊥AM，若侧棱则正三棱锥外接球的表面积是（）C48.36.32.12.DCBACRSRSAR选即,364,3,3223SABCMN题目：解析：34.9.32.3.DCBAC巩固练习从P点出发三条射线PA，PB，PC两两成60°，且分别与球O相切于A，B，C三点，若球的体积为，则OP的距离为（）34axxaaPOPHPA26,36,22即0PABCHPABCO因PA与球O相切于点A，∴OA⊥PA,同理，OB⊥PB,OC⊥PC.∴RtΔPOA≌RtΔPOB≌RtΔPOC∴PA=PB=PC又∠APB=∠BPC=∠CPA=60°∴ΔPAB、ΔPBC、ΔPCA、ΔABC为全等的等边三角形，∴P---ABC为正四面体；O---ABC为正三棱锥。解析：先想象一下图形，画出示意图由已知得球半径R=1，设PA=a，OP=x，设P在底面ABC上的射影为H（也是O在底面ABC上的射影），则AH⊥PH.在RtΔPAO中，有：222221,xaPOAOPA即又3,2,2,234612222xaaaaa2.21.3.2.DCBAB§4球与棱柱切接问题举例正三棱柱的外接球球心在上下底面中心连线的中点。ΔAOB是等腰三角形，OA=OB=ROABCA1B1C1M222dr21d33r,tRhOMaAMROAAOMR，，，中在设球半径为R，球心到底面ABC的距离为d，ΔABC的外接圆半径为r.设正三棱柱高AA1=h，底...