曲线的曲率和Frenet标架VIP免费

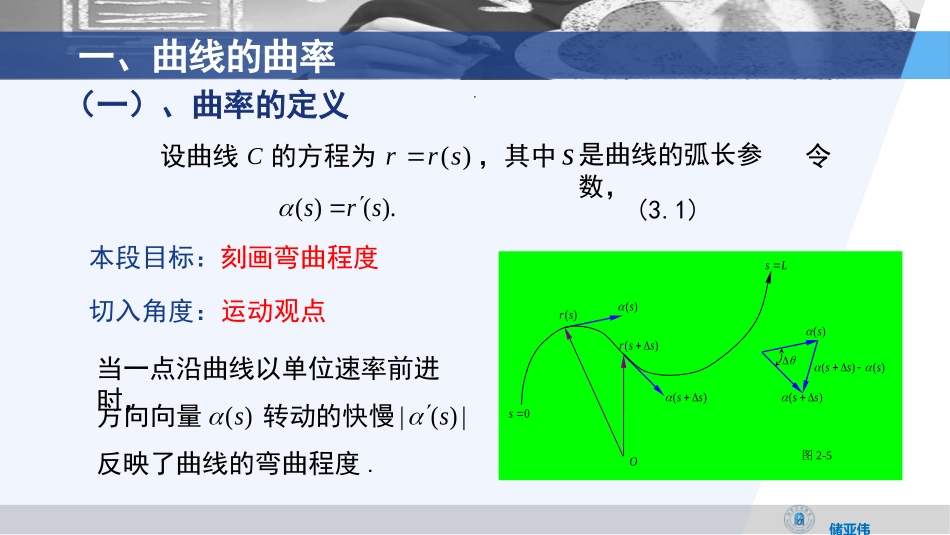
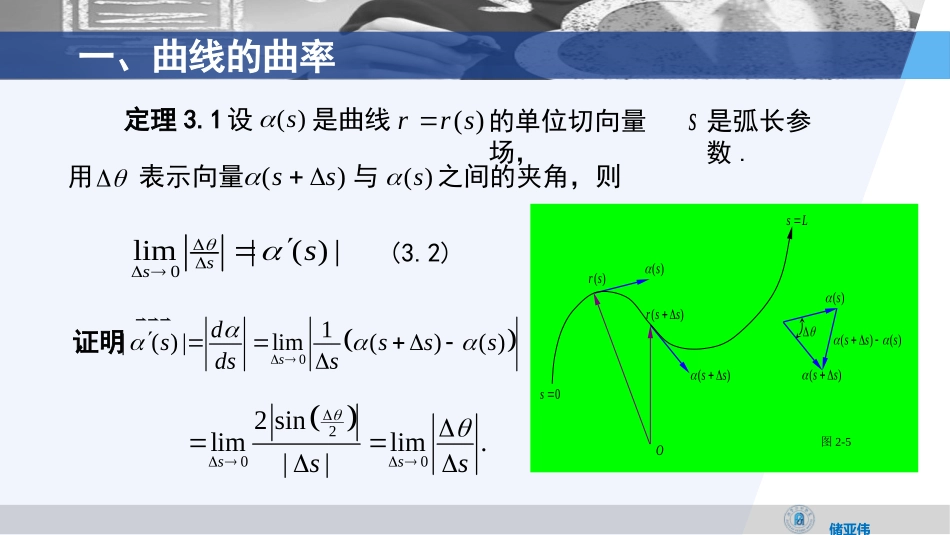
微分几何储亚伟©Copyright第二章曲线论§2.3曲线的曲率和Frenet标架储亚伟一、曲线的曲率.（一）、曲率的定义设曲线C的方程为()rrs，其中s是曲线的弧长参数，令()().srs(3.1)本段目标：刻画弯曲程度()rs0s图2-5O()ssL()ss()rss()ss()s()()sss切入角度：运动观点当一点沿曲线以单位速率前进时，反映了曲线的弯曲程度.()s方向向量转动的快慢|()|s储亚伟一、曲线的曲率定理3.1设()s是曲线()rrs的单位切向量场，s是弧长参数.0lim|()|sss(3.2)证明01|()|lim()()sdssssdss2002sinlimlim.||ssss()rs0s图2-5O()ssL()ss()rss()ss()s()()sss表示向量()ss与()s之间的夹角，则用储亚伟一、曲线的曲率定义：在称函数():|()|ss为曲线()rrss点处的曲率，把曲线C的单位切向量()s平移到原点，其端点所描出的曲线称为曲线的切线象，其方程是如圆柱螺线的切线象是单位球面上圆柱螺线的切线象2()圆柱螺线()(cos,sin,)rtatatbt()(sin,cos,)rtatatb221()(sin,cos,)abtatatb(0)(0)2()()()32()32()()s为该曲线的曲率向量.称()s(3.3)的一个圆.实例：直线、圆.储亚伟一、曲线的曲率（二）、曲率的几何意义当然，s不一定是切线象的弧长参数.切线象()s的弧长为|()|()dssdssds(3.4)所以dsds(3.5)即曲率是切线象的弧长元素与曲线的弧长元素之比.定理3.2曲线为直线的重要条件是其曲率为零.储亚伟二、Frenet标架（一）、Frenent标架的定义1.法向量场2.主法向量场如果在一点s处()0s，则向量11()|()|()()()sssss称为曲线在该点的主法向量.于是在该点有由|()|1()()0,sss所以曲率向量()s是曲线的一个法向量场.()()(),sss(3.6)储亚伟二、Frenent标架3.次法向量场在()0s处，令()()(),sss(3.7)它是曲线的第二个法向量场，称为在该点的次法向量(副法向量).这样，在正则曲线上()0s的点，有一个完全确定的正交标架();(),(),()rssss称为曲线在该点的Frenet标架，它的确定不受曲线的保持定向的参数变换的影响.储亚伟二、Frenent标架注意：如果在一点0s处0()0s则一般来说无法定义在该点的Frenet标架.1.若()0,sC则是直线，可以定义它的Frenet标架.0s0s2.若是的孤立零点，则在的两侧都有Frenet标架如果00()()ss0s，则可以将Frenet标架延拓到点.3.在其他的情况下将曲线分成若干段来考察.切线、主法线和次法线，法平面、从切面和密切面的定义与方程：储亚伟二、Frenent标架切线：()()();ursus[()]()0;Xrss�法平面：[()]()0.Xrss�密切面：密切平面法平面从切平面切线主法线次法线()s()s()s()rs[()]()0;Xrss�从切面：()()();ursus主法线：()()();ursus次法线：（二）、标架相关的线面方程储亚伟三、曲率与Frenet标架的计算3|()()|();|()|rtrttrt;()();|()()|rtrtrtrt();|()|rtrt()|()|.dsstrtdt证明()sst设为弧长参数，()tts为其反函数.则由(2.4)（一）、弧长参数下的计算公式()|()||()|;ssrs()();drssds()();|()|rssrs�()()().|()|rsrssrs...