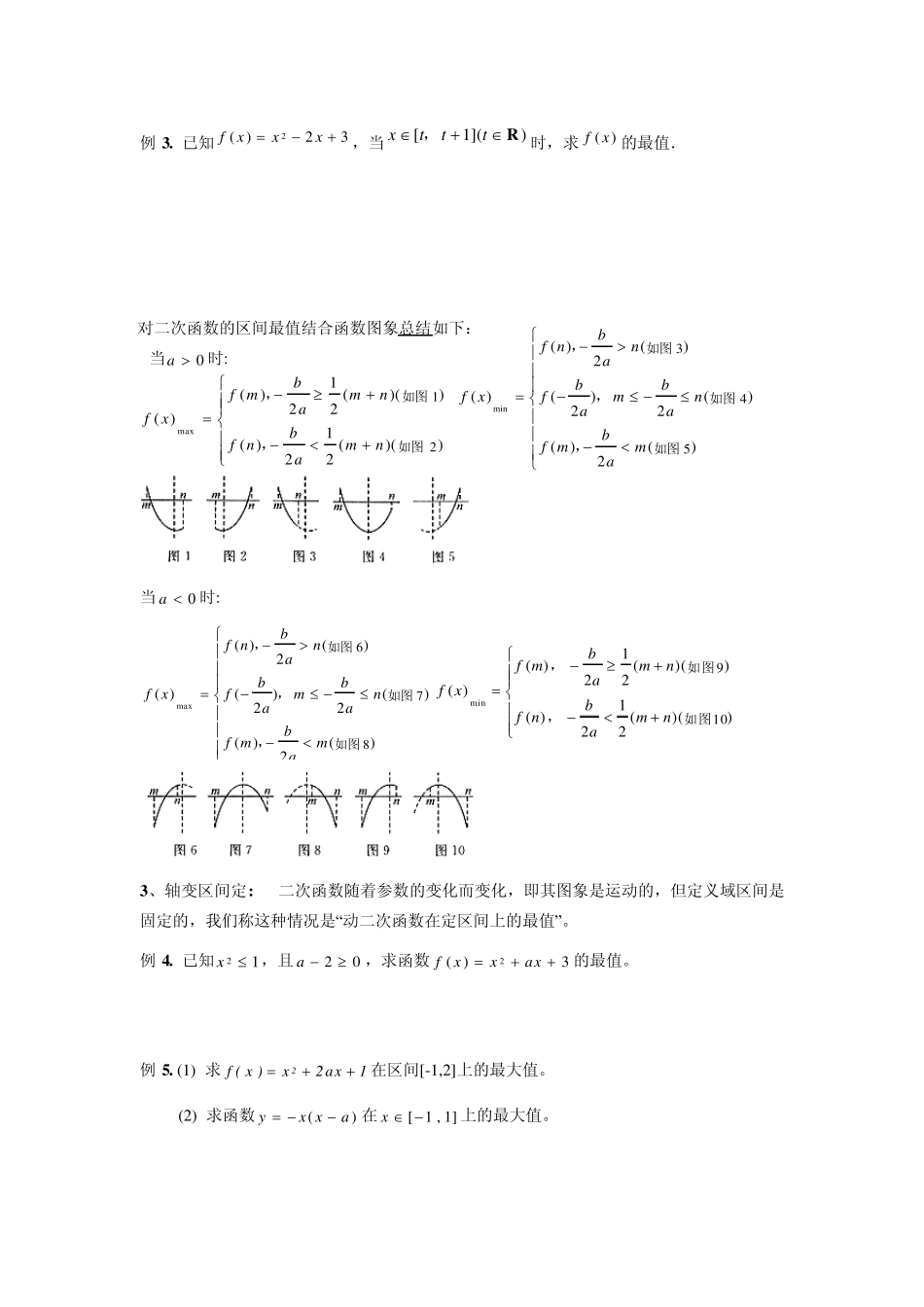
二次函数在闭区间上的最值 一、 知识要点: 一元二次函数的区间最值问题,核心是函数对称轴与给定区间的相对位置关系的讨论。一般分为:对称轴在区间的左边,中间,右边三种情况. 设 fxaxbxc a( )()20 ,求 fx( ) 在xmn[],上的最大值与最小值。 分析:将 fx( ) 配方,得顶点为 baacba2442,、对称轴为 xba 2 当a 0 时,它的图象是开口向上的抛物线,数形结合可得在[m,n]上fx( ) 的最值: (1)当bamn2,时, fx( ) 的最小值是 fbaacbafx 2442,( ) 的最大值是fmfn()( )、中的较大者。 (2)当bamn2,时 若 bam2,由 fx( ) 在mn,上是增函数则 fx( ) 的最小值是 fm() ,最大值是 fn( ) 若 nba 2,由 fx( ) 在mn,上是减函数则 fx( ) 的最大值是 fm() ,最小值是 fn( ) 当a 0 时,可类比得结论。 二、例题分析归类: (一)、正向型:是指已知二次函数和定义域区间,求其最值。对称轴与定义域区间的相互位置关系的讨论往往成为解决这类问题的关键。此类问题包括以下四种情形:(1)轴定,区间定;(2)轴定,区间变;(3)轴变,区间定;(4)轴变,区间变。 1. 轴定区间定: 二次函数是给定的,给出的定义域区间也是固定的,我们称这种情况是“定二次函数在定区间上的最值”。 例 1 . 函数yxx 242 在区间[0,3]上的最大值是_________,最小值是_______。 练习. 已知232xx,求函数fxxx( ) 21 的最值__ _____。 2 、轴定区间变: 二次函数是确定的,但它的定义域区间是随参数而变化的,我们称这种情况是“定函数在动区间上的最值”。 例 2 . 如果函数fxx( )()112定义在区间tt, 1 上,求 fx( ) 的最值。 例3. 已知2( )23fxxx,当[1]()xttt R,时,求( )fx的最值. 对二次函数的区间最值结合函数图象总结如下: 当a 0 时: 当a 0 时: )(2)()(2)2()(2)()(876max如图如图如图,,,mabmfnabmabfnabnfxff xf mbamnf nbamn( )( )()()( )()()min ,,如图如图212212910 3、轴变区间定: 二次函数随着参数的变化而变化,即其图象是运动的,但定义域区间是固定的,我们称这种情况是“动二次函数在定区间上的最值”。 例4....