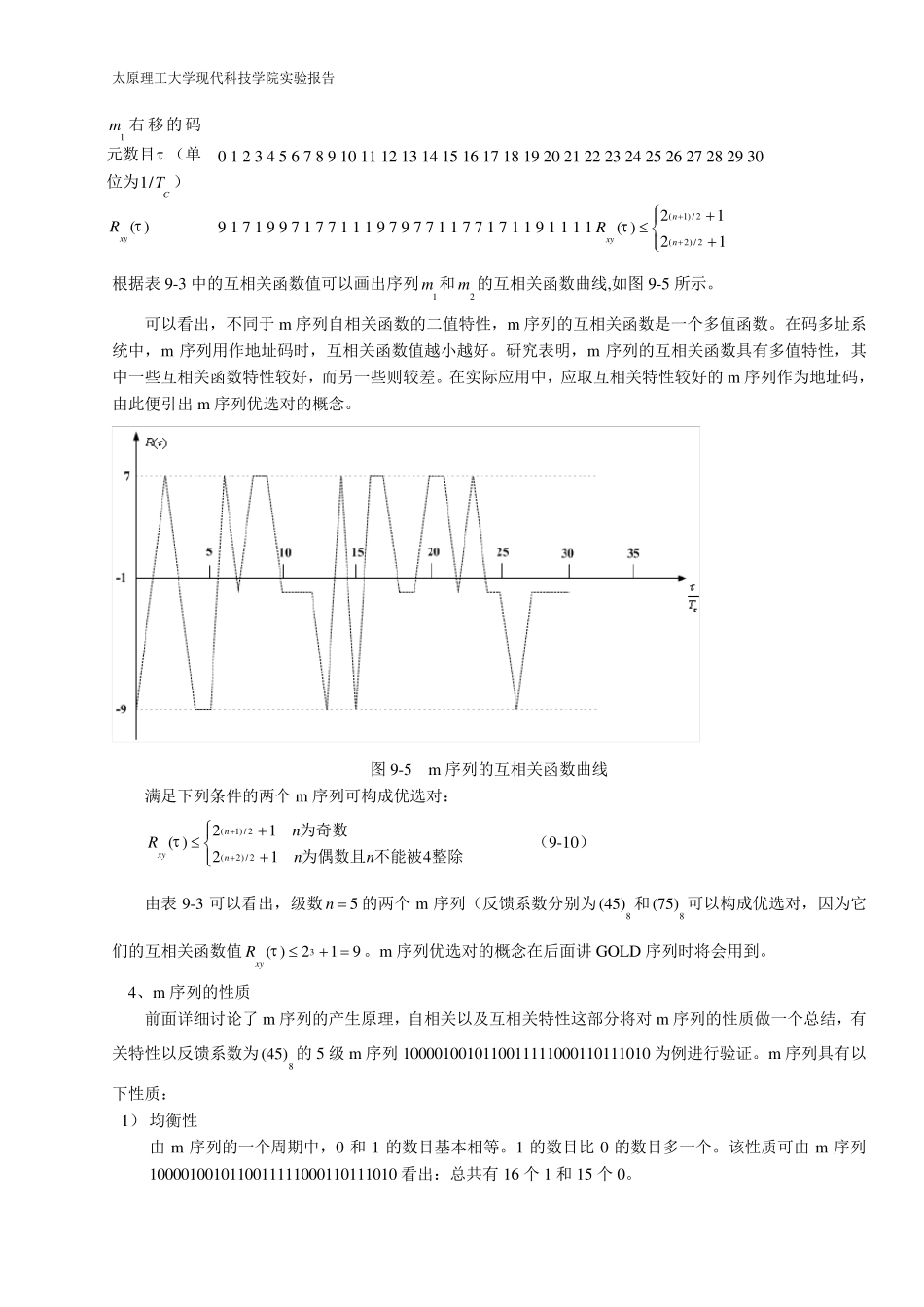
太原理工大学现代科技学院实验报告 一、实验目的 通过本实验掌握 m 序列的特性、产生方法及应用。 二、实验内容 1、观察 m 序列,识别其特征。 2、观察 m 序列的自相关特性。 三、基本原理 m序列是有n级线性移位寄存器产生的周期为 21n 的码序列,是最长线性移位寄存器序列的简称。码分多址系统主要采用两种长度的m序列:一种是周期为1521 的m序列,又称短PN序列;另一种是周期为4221 的m序列,又称为长PN码序列。m序列主要有两个功能:①扩展调制信号的带宽到更大的传输带宽,即所谓的扩展频谱;②区分通过多址接入方式使用同一传输频带的不同用户的信号。 3、m 序列的互相关函数 两个码序列的互相关函数是两个不同码序列一致程度(相似性)的度量,它也是位移量的函数。当使用码序列来区分地址时,必须选择码序列互相关函数值很小的码,以避免用户之间互相干扰。 研究表明,两个长度周期相同,由不同反馈系数产生的 m 序列,其互相关函数(或互相关系数)与自相关函数相比,没有尖锐的二值特性,是多值的。作为地址码而言,希望选择的互相关函数越小越好,这样便于区分不同用户,或者说,抗干扰能力强。 在二进制情况下,假设码序列周期为 P 的两个 m 序列,其互相关函数 Rxy(τ)为 ( )xyRAD (9-9) 式中,A 为两序列对应位相同的个数,即两序列模 2 加后“0”的个数;D 为两序列对应位不同的个数,即两序列模 2 加后“1”的个数。 为了理解上述指出的互相关函数问题,在此以5n 时由不同的反馈系数产生的两个 m 序列为例计算它们的互相关系数,以进一步讲述 m 序列的互相关特性。将反馈系数为8(45) 和8(75) 时产生的两个 5 级 m 序列分别记做:1m :1000010010110011111000110111010 和2m :111110111000101011010000110100,序列1m 和2m 的互相关函数如表9-3 所示。 表9-3 序列1m 和2m 的互相关函数表 序列1m 1 0 0 0 0 1 0 0 1 0 1 1 0 0 1 1 1 1 1 0 0 0 1 1 0 1 1 1 0 1 0 序列2m 1 1 1 1 1 0 1 1 1 0 0 0 1 0 1 0 1 1 0 1 0 0 0 0 1 1 0 0 1 0 0 太原理工大学现代科技学院实验报告 1m 右移的码元数目 (单位为1/CT ) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 ( )xyR 9 1 7 1 9 9 7 1...