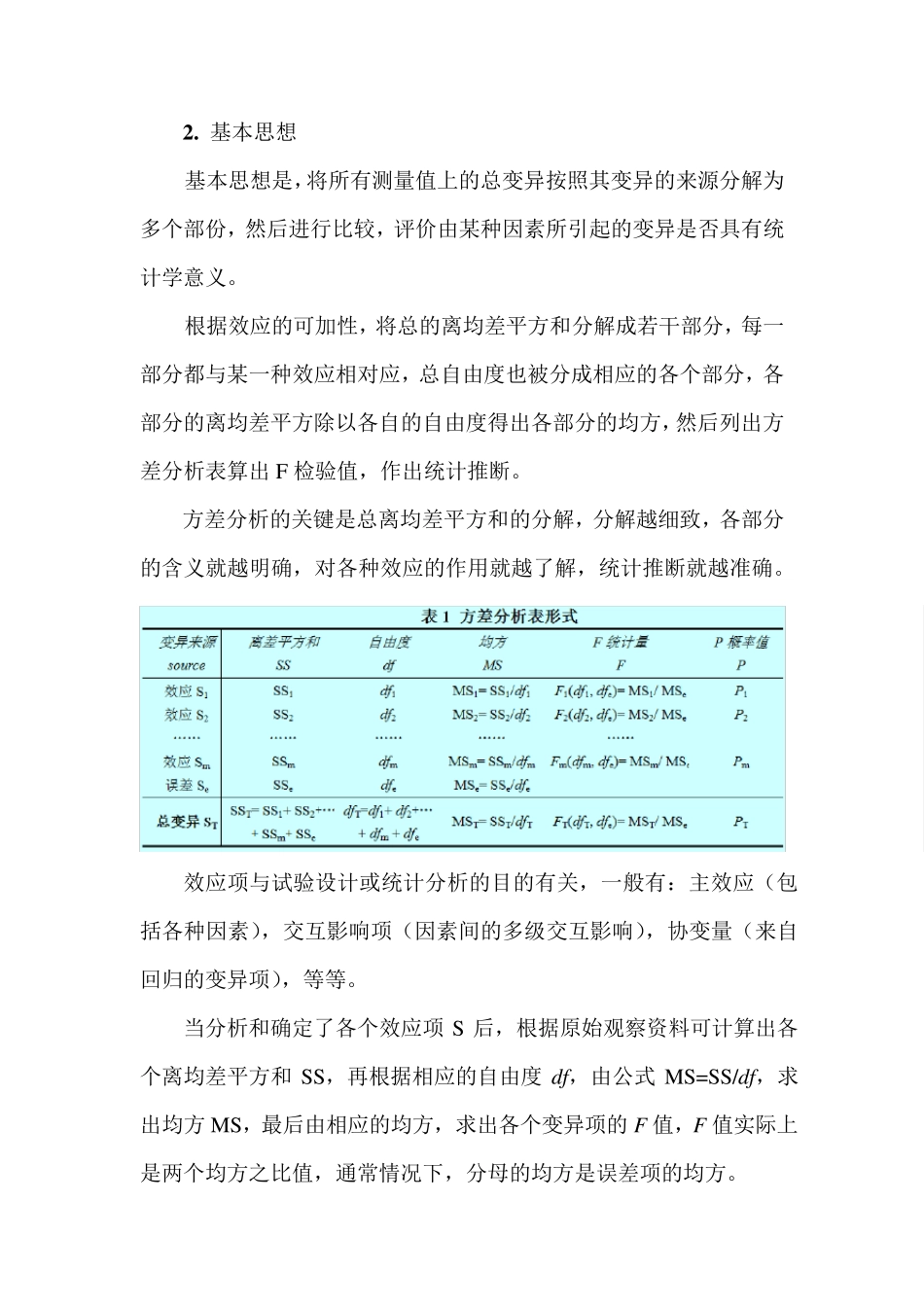
方差分析 一、方差分析原理 1
方差分析概述 方差分析可用来研究多个分组的均值有无差异，其中分组是按影响因素的不同水平值组合进行划分的
方差分析是对总变异进行分析
看总变异是由哪些部分组成的，这些部分间的关系如何
方差分析，是用来检验两个或两个以上均值间差别显著性（影响观察结果的因素：原因变量（列变量）的个数大于2，或分组变量（行变量）的个数大于1）
一元时常用F检验（也称一元方差分析），多元时用多元方差分析（最常用Wilks’∧检验）
方差分析可用于： （1）完全随机设计（单因素）、随机区组设计（双因素）、析因设计、拉丁方设计和正交设计等资料； （2）可对两因素间交互作用差异进行显著性检验； （3）进行方差齐性检验
要比较几组均值时，理论上抽得的几个样本，都假定来自正态总体，且有一个相同的方差，仅仅均值可以不相同
还需假定每一个观察值都由若干部分累加而成，也即总的效果可分成若干部分，而每一部分都有一个特定的含义，称之谓效应的可加性
所谓的方差是离均差平方和除以自由度，在方差分析中常简称为均方（Mean Square）
基本思想 基本思想是，将所有测量值上的总变异按照其变异的来源分解为多个部份，然后进行比较，评价由某种因素所引起的变异是否具有统计学意义
根据效应的可加性，将总的离均差平方和分解成若干部分，每一部分都与某一种效应相对应，总自由度也被分成相应的各个部分，各部分的离均差平方除以各自的自由度得出各部分的均方，然后列出方差分析表算出 F 检验值，作出统计推断
方差分析的关键是总离均差平方和的分解，分解越细致，各部分的含义就越明确，对各种效应的作用就越了解，统计推断就越准确
效应项与试验设计或统计分析的目的有关，一般有：主效应（包括各种因素），交互影响项（因素间的多级交互影响），协变量（来自回归的变异项），等等
当分析和确定了各
