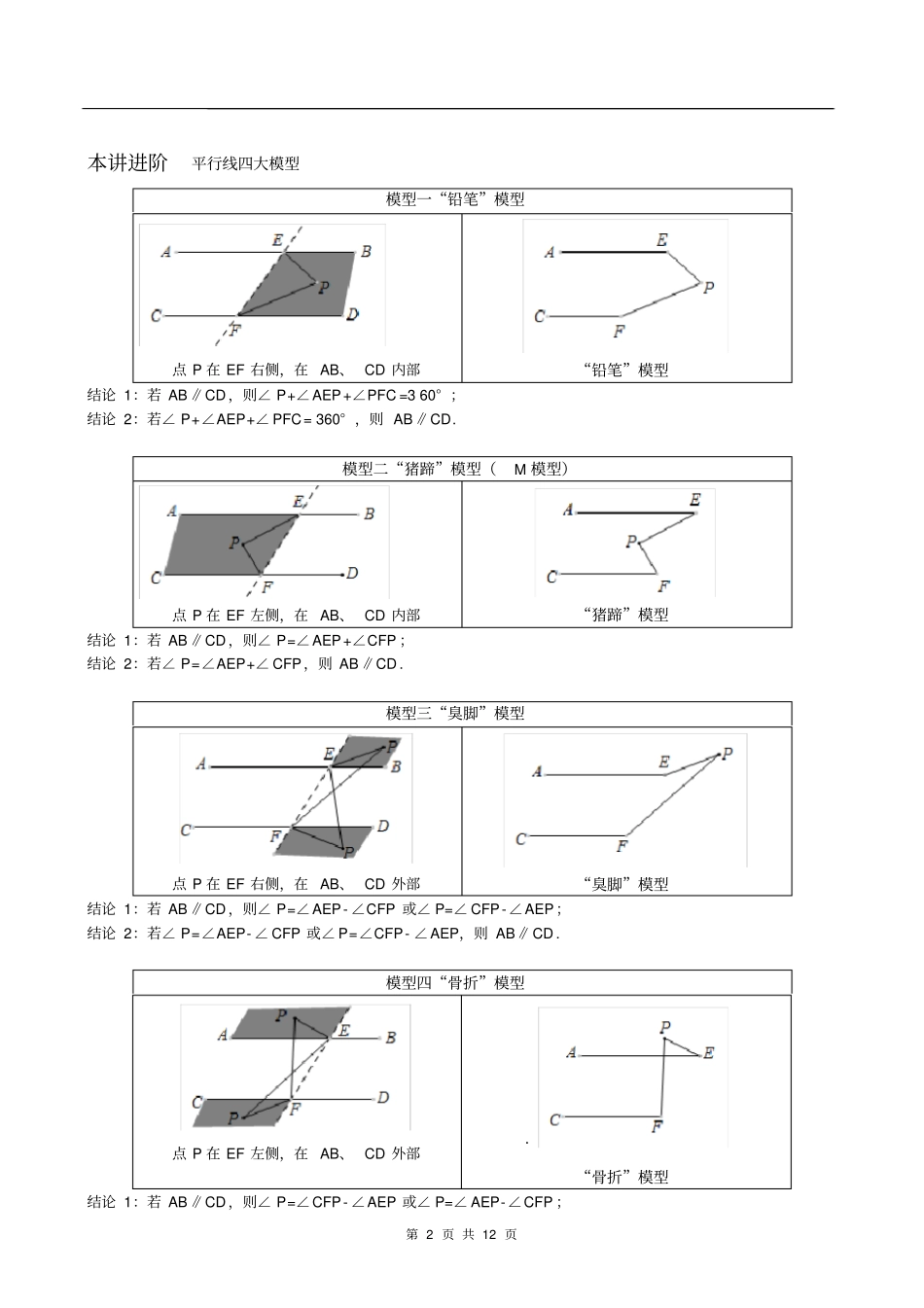
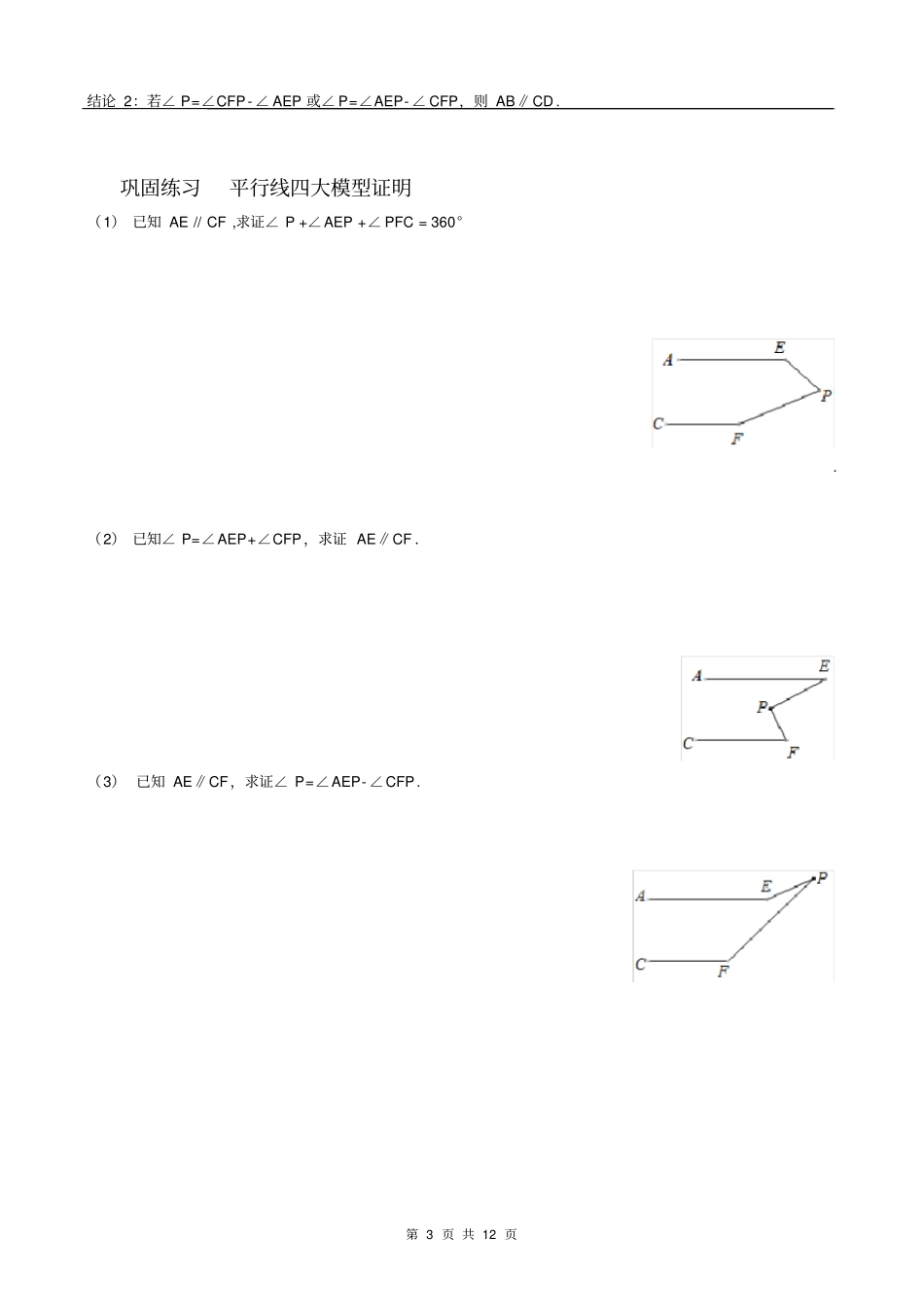
第 1 页 共 12 页平行线四大模型平行线的判定与性质l 、平行线的判定根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行,但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据定义来判断两条直线是否平行,这就需要更简单易行的判定方法来判定两直线平行.判定方法l:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简称:同位角相等,两直线平行.判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简称:内错角相等,两直线平行,判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简称:同旁内角互补,两直线平行,如上图:若已知∠ 1=∠2,则 AB∥ CD(同位角相等,两直线平行);若已知∠ 1=∠3,则 AB∥ CD(内错角相等,两直线平行);若已知∠ 1+ ∠4= 180 ° ,则 AB∥CD (同旁内角互补,两直线平行).另有平行公理推论也能证明两直线平行:平行公理推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.2、 平行线的性质利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行.反过来,如果已知两条直线平行,当它们被第三条直线所截,得到的同位角、内错角、同旁内角也有相应的数量关系,这就是平行线的性质.性质 1:两条平行线被第三条直线所截,同位角相等.简称:两直线平行,同位角相等性质 2:两条平行线被第三条直线所截,内错角相等.简称:两直线平行,内错角相等性质 3:两条平行线被第三条直线所截,同旁内角互补.简称:两直线平行,同旁内角互补第 2 页 共 12 页本讲进阶平行线四大模型模型一“铅笔”模型点 P 在 EF 右侧,在 AB、 CD 内部“铅笔”模型结论 1:若 AB∥CD ,则∠ P+∠AEP+∠PFC =3 60° ;结论 2:若∠ P+∠AEP+∠ PFC= 360° ,则 AB∥CD.模型二“猪蹄”模型(M 模型)点 P 在 EF 左侧,在 AB、 CD 内部“猪蹄”模型结论 1:若 AB∥CD ,则∠ P=∠AEP+∠CFP ;结论 2:若∠ P=∠AEP+∠ CFP,则 AB∥CD . 模型三“臭脚”模型点 P 在 EF 右侧,在 AB、 CD 外部“臭脚”模型结论 1:若 AB∥CD ,则∠ P=∠AEP- ∠CFP 或∠ P=∠ CFP-∠AEP;结论 2:若∠ P=∠AEP- ∠ CFP 或∠ P=∠CFP- ∠AEP,则 AB∥CD . 模型四“骨折”模型点 P 在 EF 左侧,在 AB、 C...