SAS讲义第二十八课Wilcoxon秩和检验VIP免费

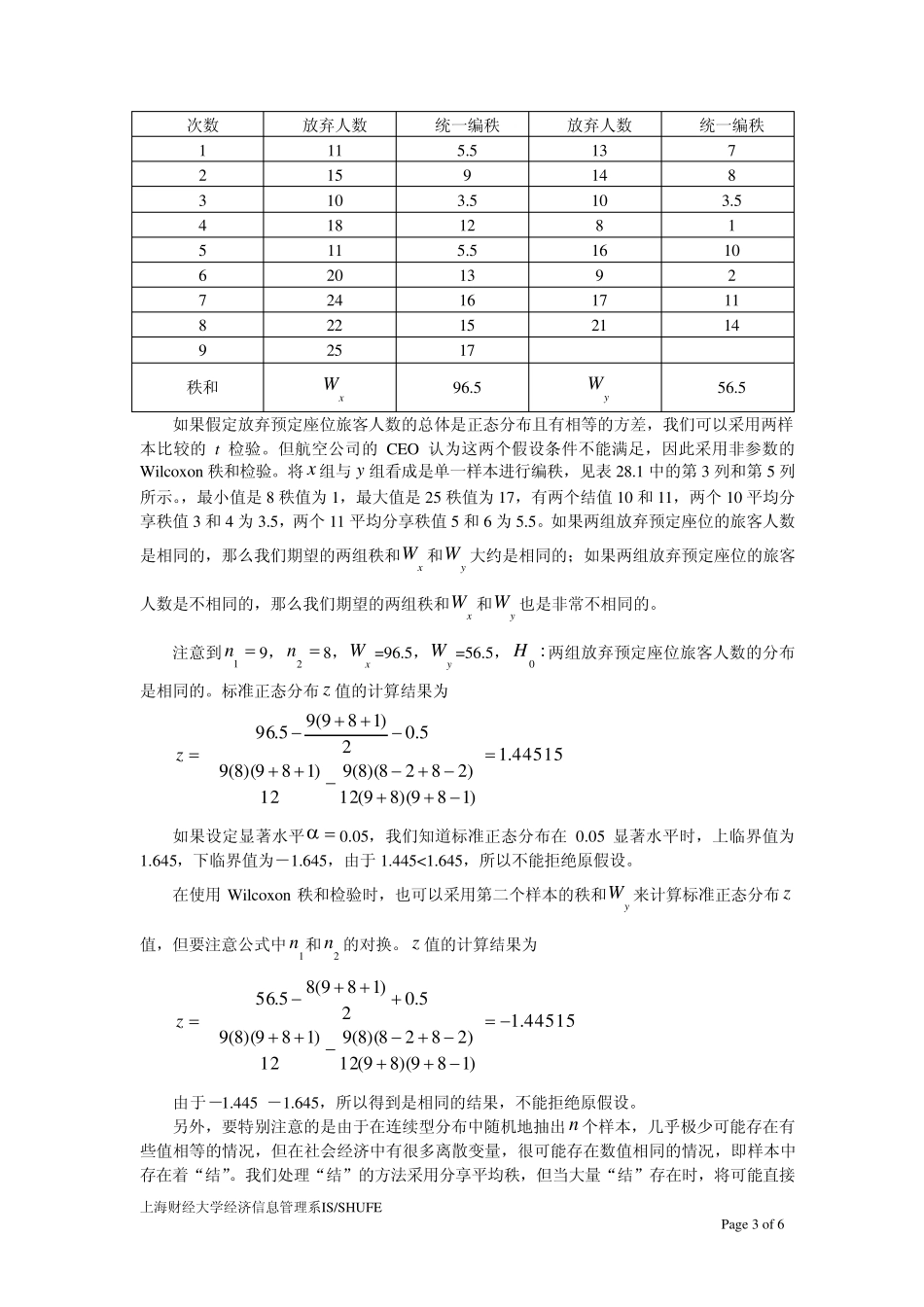
上海财经大学经济信息管理系IS/SHUFE Page 1 of 6 第二十八课 Wilcox on 秩和检验 一、 两样本的 Wilcoxon 秩和检验 由 Mann，Whitney 和Wilcox on 三人共同设计的一种检验，有时也称为 Wilcox on 秩和检验，用来决定两个独立样本是否来自相同的或相等的总体。如果这两个独立样本来自正态分布和具有相同方差时，我们可以采用 t 检验比较均值。但当这两个条件都不能确定时，我们常替换 t 检验法为 Wilcox on 秩和检验。 Wilcox on 秩和检验是基于样本数据秩和。先将两样本看成是单一样本（混合样本）然后由小到大排列观察值统一编秩。如果原假设两个独立样本来自相同的总体为真，那么秩将大约均匀分布在两个样本中，即小的、中等的、大的秩值应该大约均匀被分在两个样本中。如果备选假设两个独立样本来自不相同的总体为真，那么其中一个样本将会有更多的小秩值，这样就会得到一个较小的秩和；另一个样本将会有更多的大秩值，因此就会得到一个较大的秩和。 设两个独立样本为：第一个 x 的样本容量为1n ，第二个 y 样本容量为2n ，在容量为21nnn的混合样本（第一个和第二个）中， x 样本的秩和为xW ， y 样本的秩和为yW ，且有 2)1(21nnnWWyx (28.1) 我们定义 2)1(111nnWWx (28.2) 2)1(222nnWWy (28.3) 以 x 样本为例，若它们在混合样本中享有最小的1n 个秩，于是2)1(11nnWx，也是xW 可能取的最小值；同样yW 可能取的最小值为2)1(22nn。那么，xW 的最大取值等于混合样本的 总 秩和减 去yW 的 最 小 值 ， 即2)1(2)1(22nnnn； 同 样 ，yW 的 最 大取 值 等 于2)1(2)1(11nnnn。 所 以 ， (28.2) 和(28.3) 式 中 的1W 和2W均 为 取 值 在0与2122112)1(2)1(2)1(nnnnnnnn的变量。当原假设为真时，所有的ix 和iy 相当于从上海财经大学经济信息管理系IS/SHUFE Page 2 of 6 同一总体中抽得的独立随机样本，ix 和iy 构成可分辨的排列情况，可看成一排n 个球随机地指定1n 个为x 球另2n 个为y 球，共有1nnC种可能，而且它们是等可能的。基于这样分析，在原假设为真的条件下不难求出1W 和2W 的概率分布，显然它们的分布还是相同的，这个分布称为样本大小为1n 和2n 的Mann-Whitney-Wilcoxon 分布。 一个具有实际价值的方法是，对于每个样本中的观察数大于等于 8 的大样本来说，我...