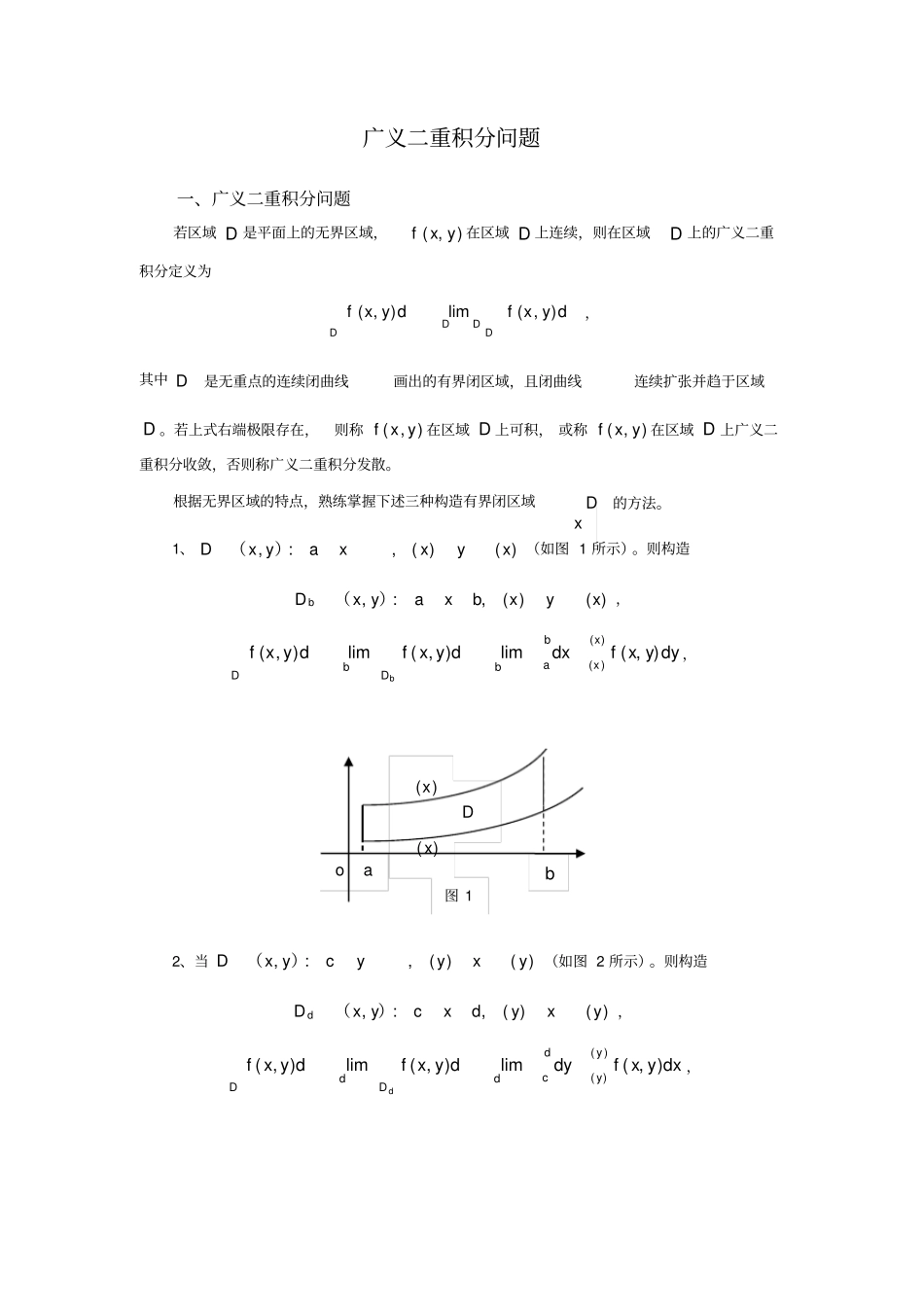
广义二重积分问题一、广义二重积分问题若区域 D 是平面上的无界区域,),(yxf在区域 D 上连续,则在区域D 上的广义二重积分定义为DDDDdyxfdyxf),(lim),(,其中 D是无重点的连续闭曲线画出的有界闭区域,且闭曲线连续扩张并趋于区域D 。若上式右端极限存在,则称),(yxf在区域 D 上可积, 或称),(yxf在区域 D 上广义二重积分收敛,否则称广义二重积分发散。根据无界区域的特点,熟练掌握下述三种构造有界闭区域D的方法。1、)()(,:,xyxxayxD)((如图 1 所示)。则构造)()(,:,xyxbxayxD b)(,)()(),(lim),(lim),(xxbabDbDdyyxfdxdyxfdyxfb,2、当)()(,:,yxyycyxD)((如图 2 所示)。则构造)()(,:,yxydxcyxD d)(,)()(),(lim),(lim),(yydcdDdDdxyxfdydyxfdyxfd,xo)(x)(xDba图 13、当区域 D 是整个 xoy平面或 xoy平面的某一象限或某一角形区域时,则构造角度变化范围)(,:,222RyxyxD R,RDRDdyxfdyxf),(lim),(,例 1 计算二重积分Dy dxdyxe2,其中 D 是由曲线2249xyxy和在第一象限所构成的无界区域,即23,0:,yxydyyxD)((如图 3 所示)。解:dyyydDydDydydxexdxdyxedxdyxed02/3/][limlim2221445]94[lim2102dyddyeyy。例 2 证明dxex2只需证明2][2dxex即可,而dyedxedxeyxx2222][,为此设)(y)(yDdc图 22yx3yxd图 3oxyRR2图 4},|),{()(}2|),{()2(};|),{()(222222RyRRxRyxRDRyxyxRRyxyxR则,)2()()(RRDR(如图 4 所示))1()1(222222222)2()()(RRyxRDyxRRyxededeede所以,当 R时,deDyx)(222][222dxedxdyexyx。因此,dxex2。