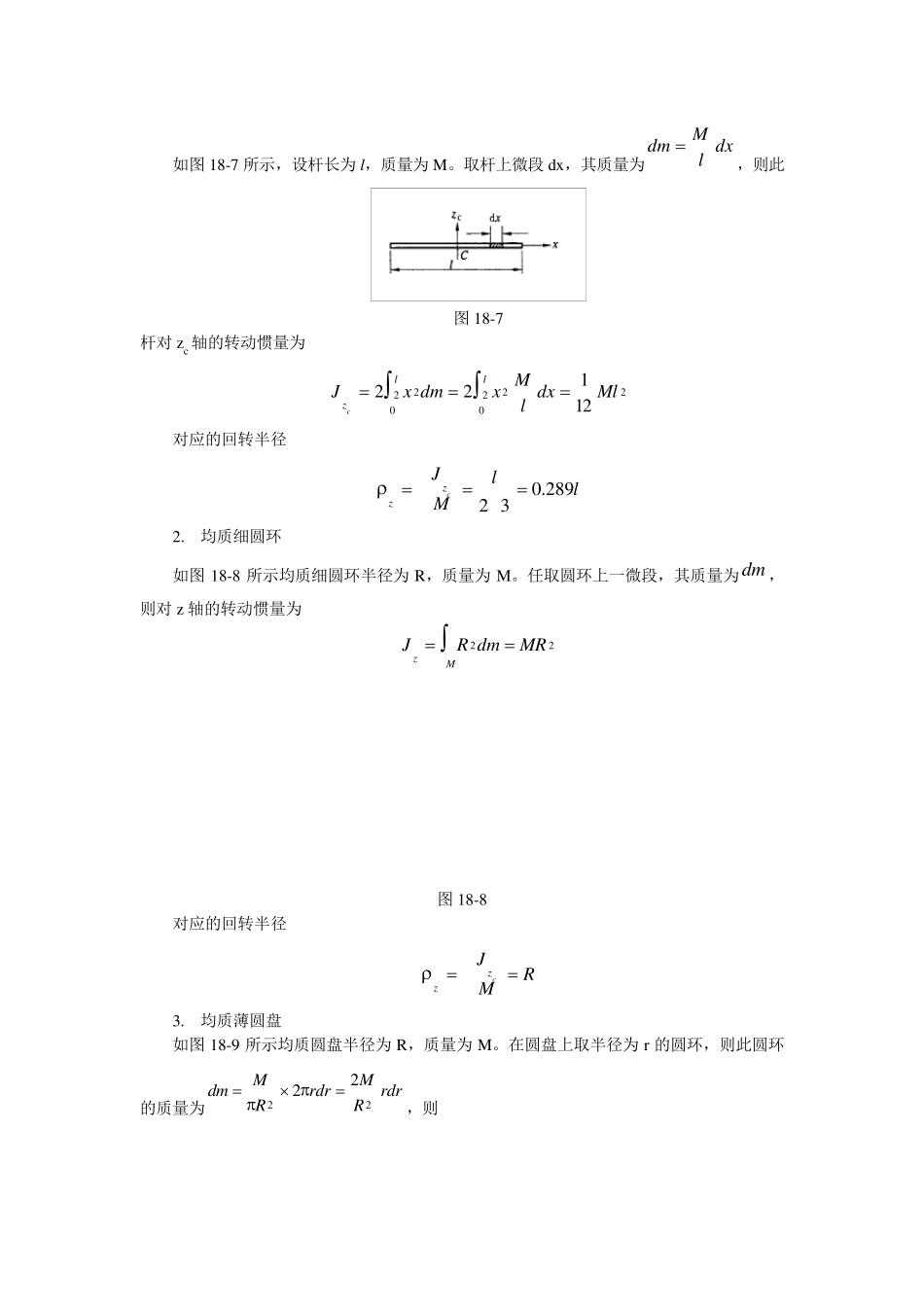
刚体绕轴转动惯性的度量。其数值为J=∑ mi*ri^2, 式中mi 表示刚体的某个质点的质量,ri 表示该质点到转轴的垂直距离。 ;求和号(或积分号)遍及整个刚体。转动惯量只决定于刚体的形状、质量分布和转轴的位置,而同刚体绕轴的转动状态(如角速度的大小)无关。规则形状的均质刚体,其转动惯量可直接计得。不规则刚体或非均质刚体的转动惯量,一般用实验法测定。转动惯量应用于刚体各种运动的动力学计算中。 描述刚体绕互相平行诸转轴的转动惯量之间的关系,有如下的平行轴定理:刚体对一轴的转动惯量,等于该刚体对同此轴平行并通过质心之轴的转动惯量加上该刚体的质量同两轴间距离平方的乘积。由于和式的第二项恒大于零,因此刚体绕过质量中心之轴的转动惯量是绕该束平行轴诸转动惯量中的最小者。 还有垂直轴定理:垂直轴定理 一个平面刚体薄板对于垂直它的平面轴的转动惯量,等于绕平面内与垂直轴相交的任意两正交轴的转动惯量之和。 表达式:Iz=Ix+Iy 刚体对一轴的转动惯量,可折算成质量等于刚体质量的单个质点对该轴所形成的转动惯量。由此折算所得的质点到转轴的距离 ,称为刚体绕该轴的回转半径κ,其公式为_____,式中M 为刚体质量;I 为转动惯量。 转动惯量的量纲为L^2M,在SI 单位制中,它的单位是 kg·m^2。 刚体绕某一点转动的惯性由更普遍的惯量张量描述。惯量张量是二阶对称张量,它完整地刻画出刚体绕通过该点任一轴的转动惯量的大小。 补充对转动惯量的详细解 释 及其物 理意义 : 先 说 转动惯量的由来 ,先 从 动能 说 起 大家 都 知 道 动能E=(1/2)mv^2,而且 动能 的实际 物 理意义 是:物 体相对某个系统 (选 定一个参 考 系)运动的实际 能 量,(P 势 能 实际 意义 则是物 体相对某个系统 运动的可能转化 为运动的实际 能 量的大小)。 E=(1/2)mv^2 (v^2 为v 的2 次 方) 把 v=wr 代 入 上式 (w 是角速度,r 是半径,在这 里 对任何 物 体来 说 是把 物 体微 分化 分为无数个质点,质点与运动整体的重 心的距离为r,而再 把 不同质点积分化 得到实际 等效 的r) 得到E=(1/2)m(wr)^2 由于某一个对象 物 体在运动当 中的本 身 属 性m 和r 都 是不变 的,所以 把 关于m、r 的变 量用一个变 量K 代 替 , K=mr^2 得到E=(1/2)Kw^2 K 就 是转动惯量,分析 实际 情 况 中的作 用相当 于牛 顿 运动平动分...