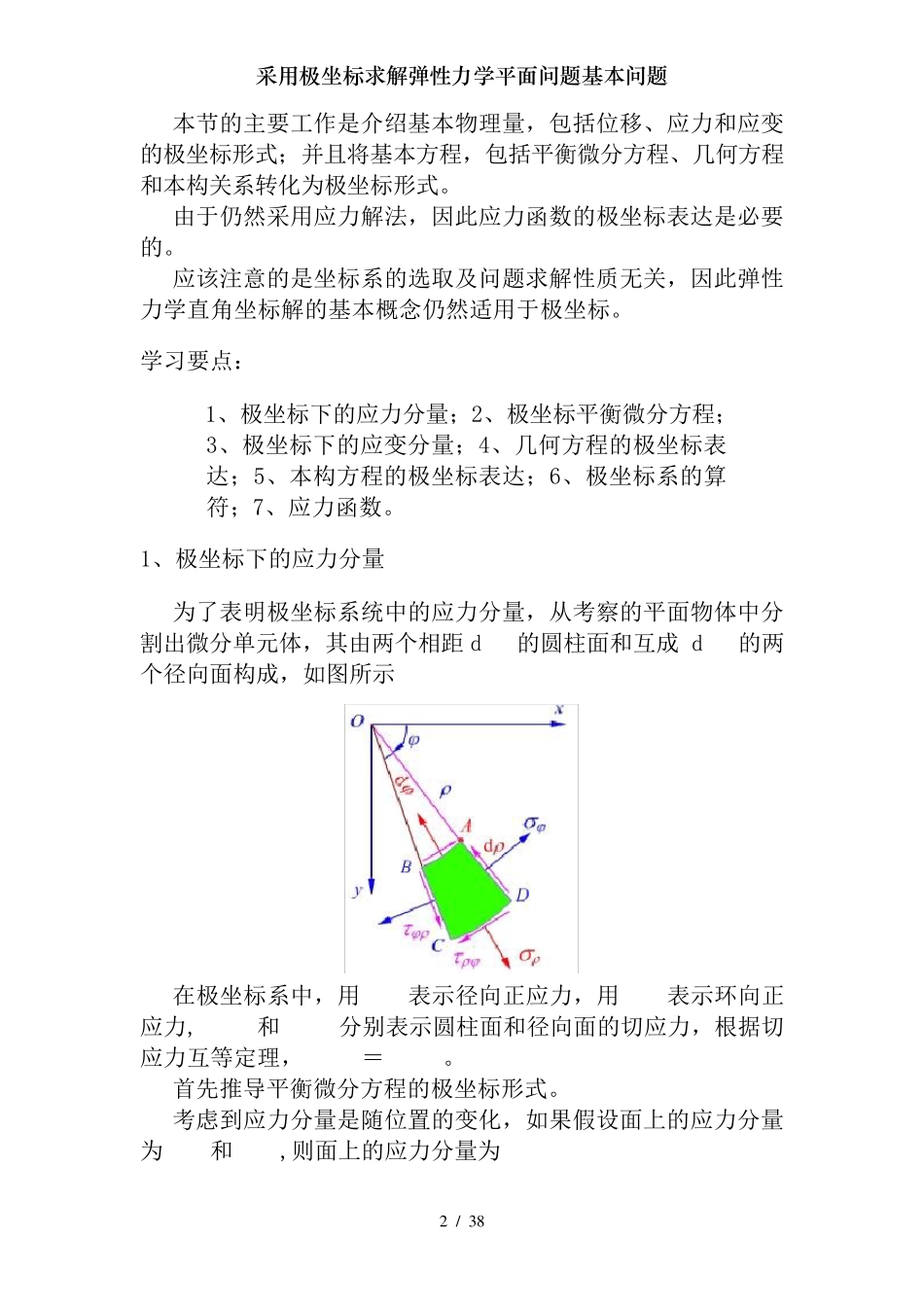
采用极坐标求解弹性力学平面问题基本问题 1 / 38 一、内容介绍 在弹性力学问题的处理时,坐标系的选择从本质上讲并不影响问题的求解,但是坐标的选取直接影响边界条件的描述形式,从而关系到问题求解的难易程度。 对于圆形,楔形,扇形等工程构件,采用极坐标系统求解将比直角坐标系统要方便的多。本章的任务就是推导极坐标表示的弹性力学平面问题基本方程,并且求解一些典型问题。 二、重点 1、基本未知量和基本方程的极坐标形式;2、双调和方程的极坐标形式;3、轴对称应力及厚壁圆筒应力;4、曲梁纯弯曲、楔形体和圆孔等典型问题 1 平面问题极坐标解的基本方程 学习思路: 选取极坐标系处理弹性力学平面问题,首先必须将弹性力学的基本方程以及边界条件通过极坐标形式描述和表达。 采用极坐标求解弹性力学平面问题基本问题 2 / 38 本节的主要工作是介绍基本物理量,包括位移、应力和应变的极坐标形式;并且将基本方程,包括平衡微分方程、几何方程和本构关系转化为极坐标形式。 由于仍然采用应力解法,因此应力函数的极坐标表达是必要的。 应该注意的是坐标系的选取及问题求解性质无关,因此弹性力学直角坐标解的基本概念仍然适用于极坐标。 学习要点: 1、极坐标下的应力分量;2、极坐标平衡微分方程;3、极坐标下的应变分量;4、几何方程的极坐标表达;5、本构方程的极坐标表达;6、极坐标系的算符;7、应力函数。 1、极坐标下的应力分量 为了表明极坐标系统中的应力分量,从考察的平面物体中分割出微分单元体,其由两个相距d 的圆柱面和互成 d 的两个径向面构成,如图所示 在极坐标系中,用表示径向正应力,用表示环向正应力,和分别表示圆柱面和径向面的切应力,根据切应力互等定理,=。 首先推导平衡微分方程的极坐标形式。 考虑到应力分量是随位置的变化,如果假设面上的应力分量为和,则面上的应力分量为 采用极坐标求解弹性力学平面问题基本问题 3 / 38 如果面上的应力分量为和,则面上的应力分量为 。 同时,体力分量在极坐标径向和环向 方向的分量分别为和。 2、极坐标平衡微分方程 设单元体的厚度为1,如图所示 考察其平衡 首先讨论径向的平衡,注意到 ,可以得到 采用极坐标求解弹性力学平面问题基本问题 4 / 38 简化上式,并且略去三阶微量,则 同理,考虑微分单元体切向平衡,可得 简化上式,可以得到极坐标系下的平衡微分方程,即 3、极坐标下的应变分量 以下推导极坐标系统的...