工科物理大作业05真空中的静电场VIP免费

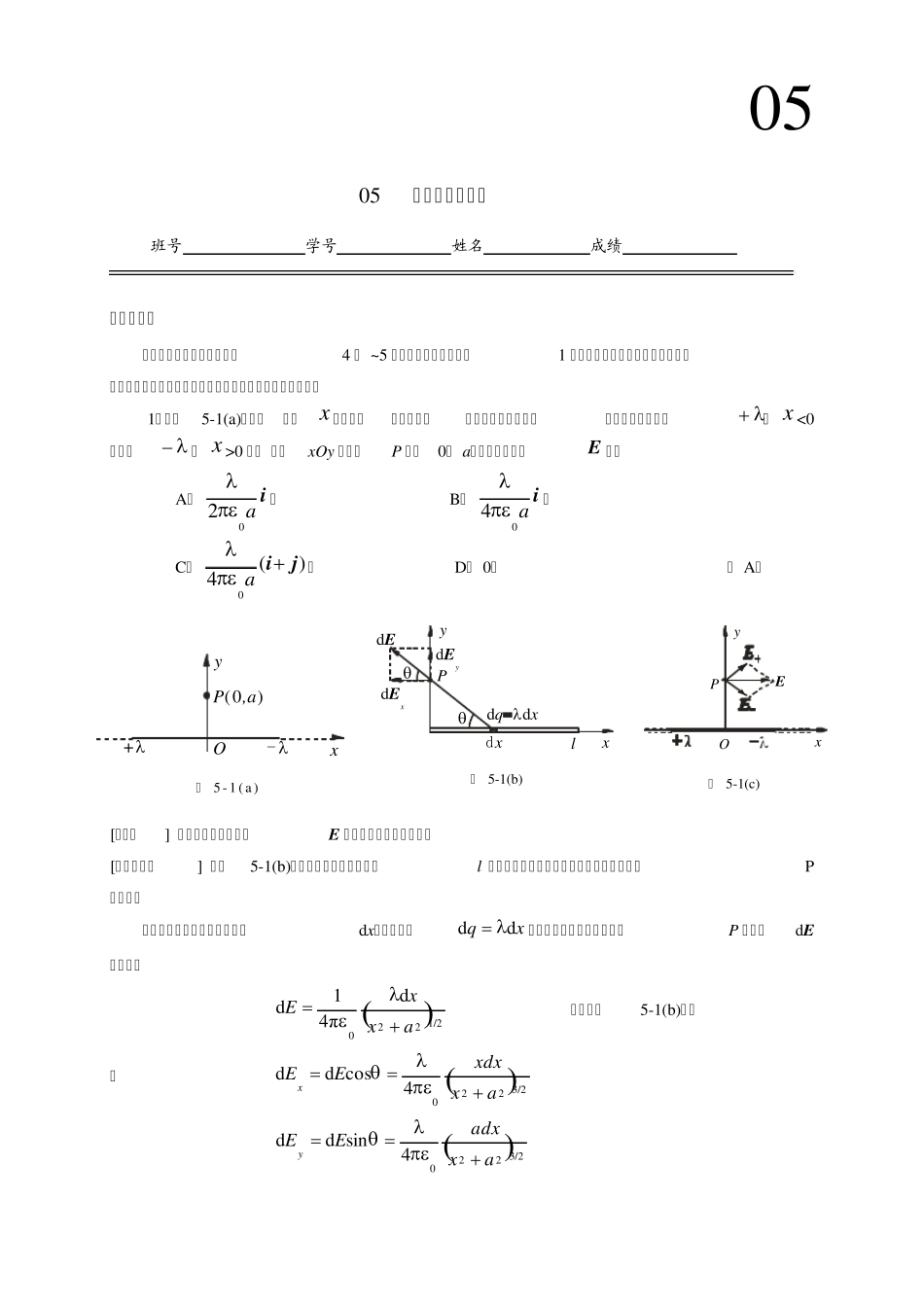
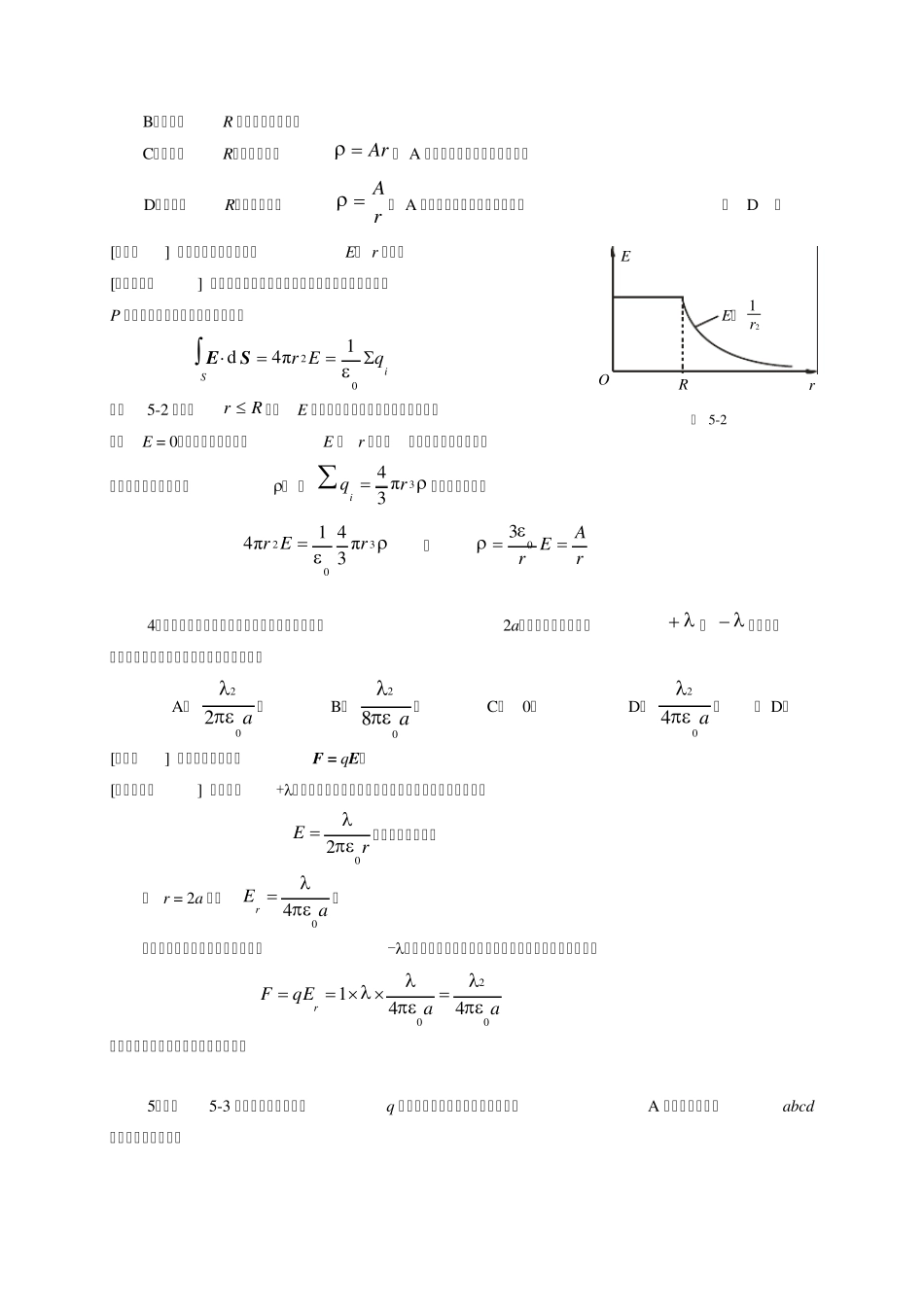
xP,a(0)O+-y 图 5 - 1 ( a ) yxddqxdEdExdEyPldx 图 5-1(b) yxEPO 图 5-1(c) 05 05 真空中的静电场 班号 学号 姓名 成绩 一、选择题 （在下列各题中，均给出了4 个 ~5 个答案，其中有的只有1 个是正确答案，有的则有几个是正确答案，请把正确答案的英文字母序号填在题后的括号内） 1．如图5-1(a)所示，一沿x轴放置的“无限长”分段均匀带电直线，电荷线密度分别为（ x<0处）和（ x>0 处） ，则xOy 平面上P 点（0， a）处的电场强度E 为： A．ia02； B．ia04； C．)(40jia； D． 0。 （ A） [知识点] 半无限长均匀带电杆E 的计算，场强叠加原理。 [分析与解答] 如图5-1(b)所示，先计算一根长度为l 的均匀带电直线在过其一端的垂面上任一点P的场强。 在均匀带电直线上任取一微元dx，其电荷元xqdd在过其一端的垂面上任一点P 的场强dE的大小为 1/2220dπ41daxxE 方向如图5-1(b)所示 则 3/22204cosddaxxdxEEx 3/22204sinddaxadxEEy 分别积分可得 alaaxxdxElx114422003/2220 22003/222044allaaxadxEly 当l时，可得半无限长均匀带电直线在其一端垂面上任一点场强为 aEx04， aEy04 可见yxEE，所以场强E 的方向与带电直线夹角 o45。 对于题目给出的“无限长”分段均匀的带电直线，可看作是两半无限长均匀带电直线电场的叠加，两段半无限长带电直线在P 点的场强方向如图 5-1(c)所示，迭加后的场强为 iiiiEEEaEEEx0oo22cos45cos45 2．真空中静电场的高斯定律告诉我们： A．高斯面内不包围自由电荷，则面上各点的E 的量值处处为零； B．高斯面上各点的E 与面内自由电荷有关，与面外的电荷无关； C．穿过高斯面的E 通量，仅与面内自由电荷有关； D．穿过高斯面的E 通量为零，则面上各点的E 必为零； E．高斯定律仅适用于对称性电场，不适用于电偶极子的电场。 （C） [知识点] 高斯定理的理解。 [分析与解答] 对于静电场的高斯定理内SSq01dSE的正确理解，应注意三个物理量之间的联系与区别。一是通过闭合曲面的电通量为SESE d，而穿过高斯面的电通量仅与高斯面内包围的电荷有关，与面外电荷分布无关，所以 0内Sq，...