工程力学课后详细答案VIP免费

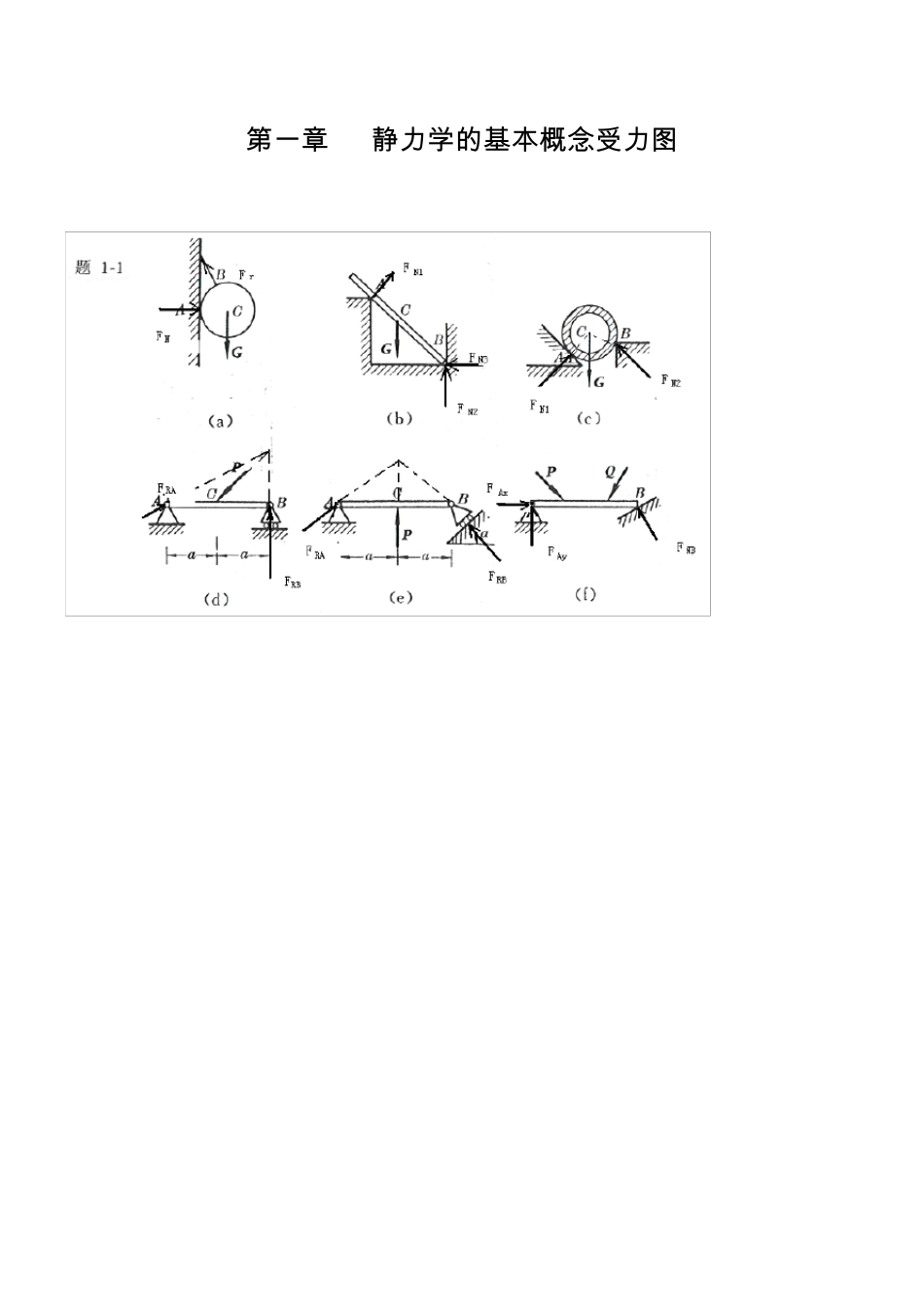
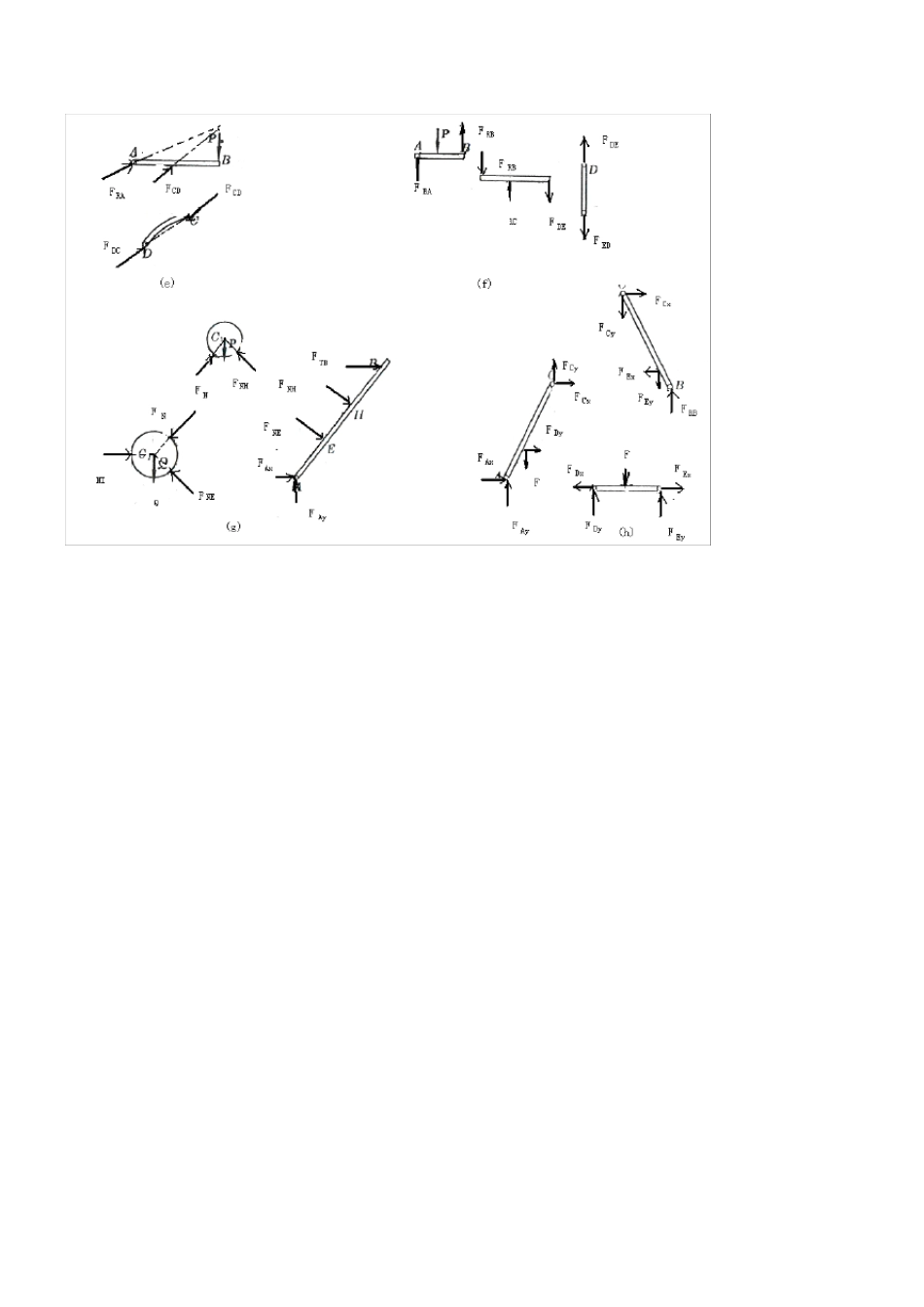
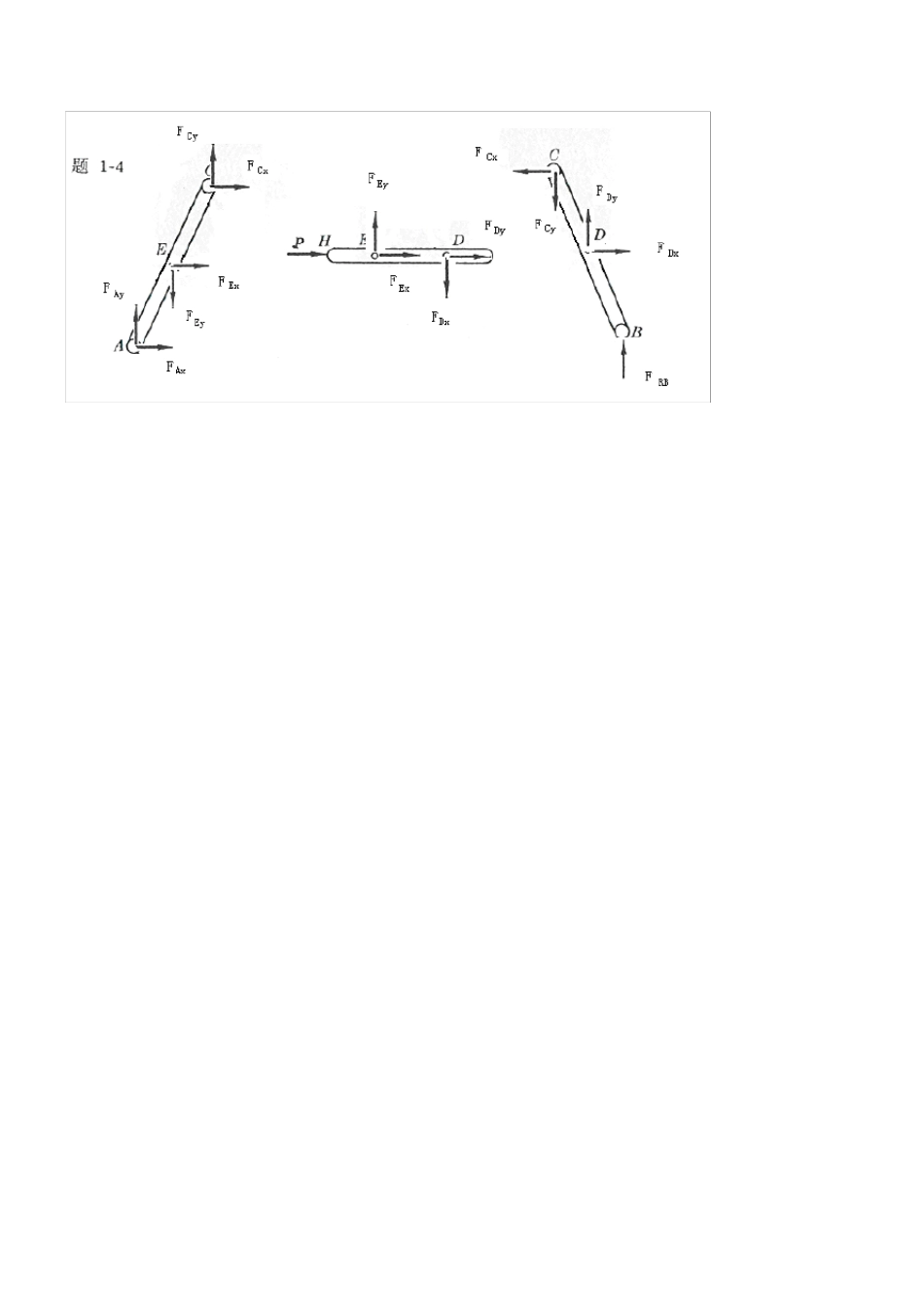
第 一章 静力学的基本概念受力图 第 二章 平面汇交力系 2-1 解：由解析法，23cos80RXFXPPN 12 sin140RYFYPPN 故： 22161.2RRXRYFFFN 1(,)arccos29 44RYRRFFPF 2-2 解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有 123cos45cos453RXFXPPPKN 13sin 45sin 450RYFYPP 故： 223RRXRYFFFKN 方向沿OB。 2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。 （a） 由平衡方程有： 0X  sin 300ACABFF 0Y  cos300ACFW 0.577ABFW（拉力）1.155ACFW（压力） （b） 由平衡方程有： 0X  cos700ACABFF 0Y  sin 700ABFW 1.064ABFW（拉力）0.364ACFW（压力） （c） 由平衡方程有： 0X  cos60cos300ACABFF 0Y  sin 30sin 600ABACFFW 0.5ABFW (拉力)0.866ACFW（压力） （d） 由平衡方程有： 0X  sin 30sin 300ABACFF 0Y  cos30cos300ABACFFW 0.577ABFW (拉力)0.577ACFW (拉力) 2-4 解：（a）受力分析如图所示： 由0x 224cos45042RAFP 15.8RAFKN 由0Y  222sin 45042RARBFFP 7.1RBFKN (b)解：受力分析如图所示：由 0x 3cos45cos45010RARBFFP 0Y  1sin 45sin 45010RARBFFP 联立上二式，得： 22.410RARBFKNFKN 2-5 解：几何法：系统受力如图所示 三力汇交于点 D，其封闭的力三角形如图示 所以： 5RAFKN （压力） 5RBFKN（与 X 轴正向夹 150 度） 2-6 解：受力如图所示： 已知，1RFG ， 2ACFG 由0x  cos0ACrFF  12cosGG 由0Y  sin0ACNFFW  22221sinNFWGWGG 2-7 解：受力分析如图所示，取左半部分为研究对象 由0x  cos45cos450RACBPFF 0Y  sin 45sin 450CBRAFF 联立后，解得： 0.707RAFP 0.707RBFP 由二力平衡定理 0.707RBCBCBFFFP 2-8 解：杆AB，AC 均为二力杆，取A 点平衡 由0x cos60cos300ACABFFW 0Y  sin 30sin 600ABACFFW 联立上二式，解得： 7.32ABFKN （受压）27.3ACFKN（受压） 2-9 解：各处全为柔索约束，故反力全为拉力，以 D，B 点分别列平衡方程 ...