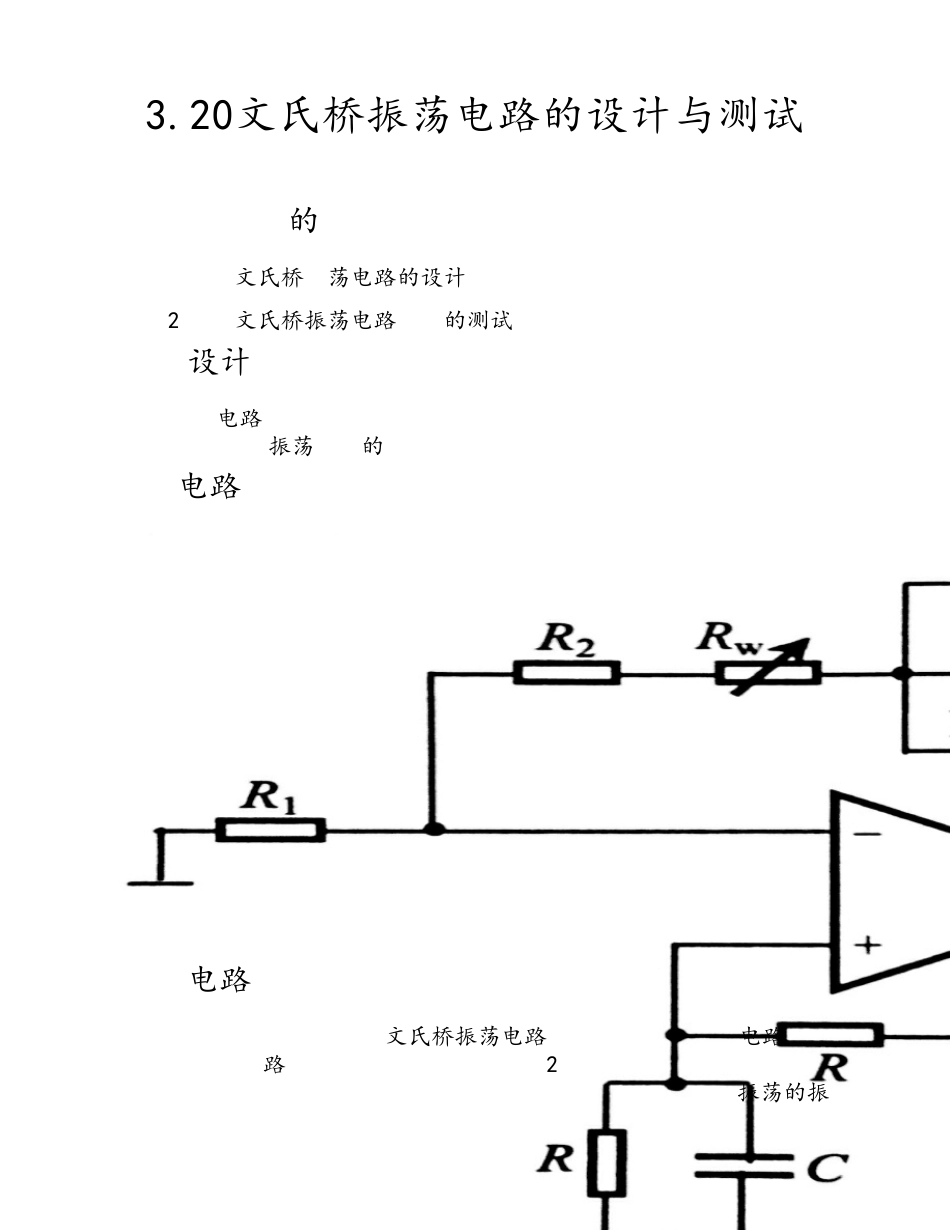
3.20文氏桥振荡电路的设计与测试 一、 实验目的1 掌握文氏桥震荡电路的设计原理。2 掌握文氏桥振荡电路性能的测试方法。二、 设计要求使电路输出从无到有,从正弦波到失真。定量绘出波形,研究RC参数对振荡频率的影响。三、电路原理图四、 电路原理如上图所示为RC文氏桥振荡电路。其中RC串、并联电路构成正反馈支路,并起选频作用,R1、R2、Rw及二极管等元件构成负反馈和稳幅条件。调解Rw可以改变负反馈深度,以满足振荡的振幅条件和改善波形。利用两个反向并联二极管D1、D2正向电阻的非线性特性来实现稳幅。D1和D2要求特性匹配,以确保输出波形正、负半周期对称。R3的接入是为了消弱二极管的影响,改善波形失真。电路的振荡频 率:f=1/2πRC 起振的幅值条件:Af=1+Rf/R1>=3 。调整Rw,使得电路起振,且失真最小。改变选频网络的参数C或R,即可调解振荡频率。五、实验内容 1.文氏桥振荡器的实现电路图:此时未起振调节R4,至R4=1K×17%=170欧时,电路开始振荡,电路其他参数不发生改变。 × 当R4=770欧 时,如图,输出没有明显失真。 当R4=790欧 时,如图,输出开始出现失真,此时振幅为10 V. 负反馈强弱对起振条件及输出波形的影响的分析: 由起振的幅值条件:Af=1+Rf/R1 >=3 和实验结果可知(1)当负反馈较弱即R4较小时,Af<3,不能起振;(2)当负反馈较强即R4较大时,由于直流源电压和运放的限制,负反馈越强,失真越严重。2.研究RC参数对振荡频率的的影响(1)R=1000欧,C=1uF时 ,如图,周期T=548.630-542.228=6.402ms,所以 频率 f1=1/T= 156.2 Hz (2)R=1000欧,C=10uF时 ,如图,周期T=835.272-771.636=63.64ms,所以 频率 f2=1/T= 15.7 Hz(3)R=100欧,C=1uF时 ,如图,周期T=56.293-55.638=0.655 ms,所以 频率 f3=1/T= 1526.7 Hz (4)R=10千欧,C=1uF时 ,如图,周期T=776.474-713.216=63.26ms,所以 频率 f4=1/T= 15.81 Hz 从实验结果可以总结出,当R或C增大时,f会减小;同理,当R或C减小时,f会增大。这与振荡频率的计算公式 fo= 相符。3.稳幅作用分析 断开D1、D2,R=1千欧,C=1uF,此时由下图可知,最大不失真波形对应的R4=520欧,比有二极管时的相应R4小。 可见,二极管对此电路有稳幅作用,有缓解输出电压失真的作用。