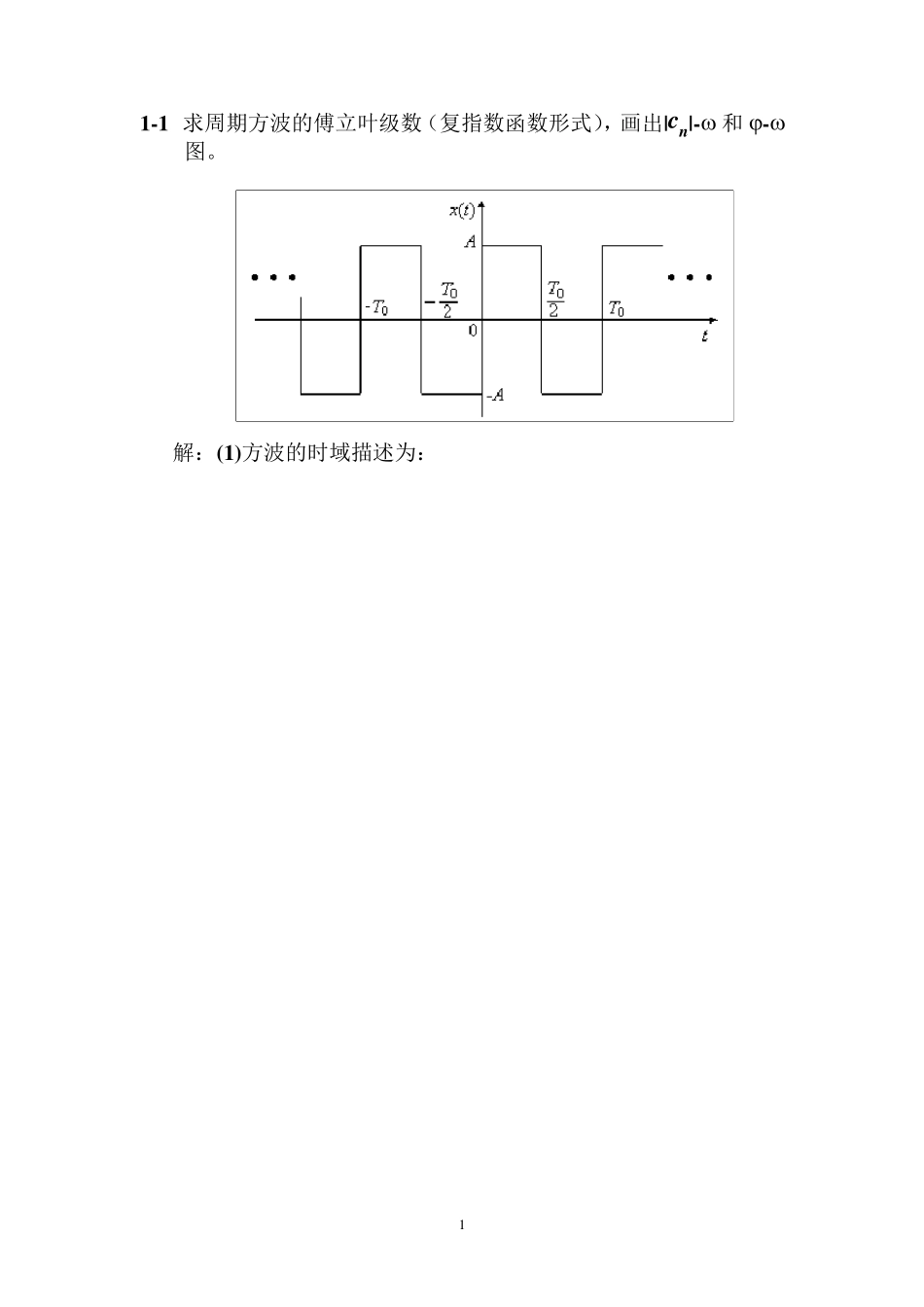
1 1-1 求周期方波的傅立叶级数(复指数函数形式),画出|cn|- 和-图。 解:(1)方波的时域描述为: 2 (2 ) 从而: 3 1 -2 . 求正弦信号 的绝对均值 和均方根值 。 解(1 ) (2 ) 1 -4 .求符号函数和单位阶跃函数的频谱。 解:(1 )因为不满足绝对可积条件,因此,可以把符合函数看作为双边指数衰减函数: 其傅里叶变换为: 4 (2 )阶跃函数: 5 1 -5 . 求被截断的余弦函数 的傅里叶变换。 解: (1 )被截断的余弦函数可以看成为:余弦函数与矩形窗 的点积,即: (2 )根据卷积定理,其傅里叶变换为: 1 -5 .求被截断的余弦函数 的傅立叶变换。 6 解:方法一: 方法二: (1 ) 其中 为矩形窗函数,其频谱为: 7 (2 )根据傅氏变换的频移性质,有: 1 -6 . 求指数衰减函数 的频谱函数 ,( )。并定性画出信号及其频谱图形。 解:(1)求单边指数函数 的傅里叶变换及频谱 (2)求余弦振荡信号 的频谱。 利用 函数的卷积特性,可求出信号 的频谱为 8 其幅值频谱为 a a` b b` c c` 题图 信号及其频谱图 9 注:本题可以用定义求,也可以用傅立叶变换的频移特性求解。 1-7.设有一时间函数 f(t)及其频谱如图所示。现乘以余弦函数 cos0t(0>m)。在这个关系中函数 f(t)称为调制信号,余弦函数 cos0t称为载波。试求调幅信号的f(t)cos0t傅氏变换,并绘制其频谱示意图。又:若 0<m 将会出现什么情况? 解:(1)令 (2) 根据傅氏变换的频移性质,有: 频谱示意图如下: (3) 当 0<m 时,由图可见, 出现混叠,不能通过滤波的方法提取出原信号 f(t)的频谱。 1 0 3-3 金属应变片与半导体应变片在工作原理上有何不同? 答:前者利用金属形变引起电阻的变化;而后者是利用半导体电阻率变化引起电阻的变化(压阻效应)。 4-1. 以阻值1 2 0R ,灵敏度S=2 的电阻丝应变片与阻值为1 2 0 的固定电阻组成电桥,供桥电压为3 V ,并假定负载为无穷大,当应变片的应变为2με和2000με是,分别求出单臂、双臂电桥的输出电压,并比较两种情况下的灵敏度。 解:(1)对于电阻型应变片来说, gdRSR 当应变片的应变为2 时: 单臂电桥的输出电压为: 66002221 0331 0444gySRUUUVR 双臂电桥的输出电压为: 66002221 0361 0222gySRUUUVR ...